来源：机器学习算法与自然语言处理

本文图文结合，建议阅读7分钟。

本文为你详细描述SVM产生的过程。

前言

众所周知 SVM 是非常强大的一种分类算法，有着媲美神经网络的分类效果，实现过程却简单得多。受限于我的能力，这篇文章不会系统地介绍 SVM（因为我并不是线性代数、凸优化等方面的专家），而是以一个学习者的角度描述 SVM 产生的过程，由于内容较长，计划分成三到四篇

一个好的分类是怎么样的

图中的两组数据，显然它们是线性可分（linear separable）的，图里给出的三条分界线都可以准确区分这两类数据，它们是不是一样好？如果不是，哪一条看起来更加合适？

直觉告诉我们是 a。相比之下，b 和 c 离个别点太近了，我们很难拍着胸脯说“这个点在分界线下面，所以绝对是 X"，因为分界线稍微挪一挪就可以改变这些点的属性，我们想要的是一个相对自信的分界线，使靠近分界线的点与分界线的距离足够大，上图中的分界线 a 就符合我们的需求。

ps. 这里所说的分界线严格来说是 decision boundary，decision boundary 在二维空间是一条线，在三维空间是一个平面，更高维的空间里称作超平面，为了方便本文都用分界线来代表 decision boundary。

进入向量的世界

你或许已经注意到 SVM 的全称是 Support Vector Machine（支持向量机），在推导 SVM 公式过程中，我们几乎都是在和向量打交道。刚接触 SVM 的时候我对这个名字非常诧异，SVM 很强是没错，但是名字也太「随意」了吧？希望写完这篇文章以后我能理解为什么这种算法叫做支持向量机。

如果你之前没有接触过向量，建议花一个小时左右的时间熟悉一下向量的概念和基本性质。我们先把空间上的点用向量来表示（以原点为起点的向量）：

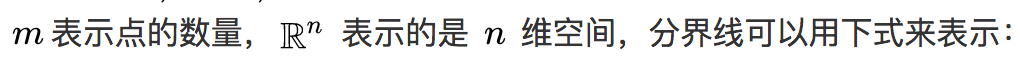
虽然写成了向量的形式，其实并没有什么大不了的，我们可以把它和初中时候学过的直线表达式联系起来：

对于 SVM 来说仅仅这样是不够的，还记得吗我们要修一条路出来，我们得确保在一条足够宽的路里面没有数据点：

这样前面的式子就可以写成更为简洁的形式：

什么是支持向量

这是一个基于 KKT 条件的二次规划问题，优化原理的内容超出了这篇文章的范畴，在这里我们只要知道拉格朗日乘数法可以求得这个最优解，引入新的系数αi :

令以上两式为0，我们可以得到：