目录

• 1 定义
• 2 常用公式推导
• • 2.1 sin²θ + cos² = 1
  • 2.2 sinθ = cos(90°-θ)、 cosθ = sin(90°-θ)
  • 2.3 sin(-θ) = -sinθ、 cos(-θ) = cosθ
  • 2.4 sin(90°+θ) = cosθ 、cos(90°+θ)=-sinθ
  • 2.5 余弦定理
  • 2.6 正弦定理
  • 2.7 cos⁡(θ-β) = cosθ*cosβ + sinθ*sinβ
• 3 三角函数图像性质
• 4 Unity中三角函数常用到的地方

1 定义

三角函数的定义：在一个平面直角坐标系中，以原点为圆心，1为半径画圆，交x轴于A点。以圆心O为旋转中心，将A点逆时针旋转θ度(一般规定逆时针旋转为正方向)至点B，设此时B点的坐标为(x, y)。
那么此时，y的值就叫做θ的正弦，记作sinθ。
x的值就叫做θ的余弦，记作cosθ。
y/x的值就叫做θ的正切，记作tanθ。

2 常用公式推导

2.1 sin²θ + cos² = 1

因为上图中单位圆上点满足x²+y²=1，又x=sinθ，y=cosθ。
所以sin²θ+cos²θ=1。

2.2 sinθ = cos(90°-θ)、 cosθ = sin(90°-θ)

如上图，θ+β=90°。
则有sinθ=y=cosβ=cos(90°-θ)。
cosθ=x=sinβ=sin(90°-θ)。

2.3 sin(-θ) = -sinθ、 cos(-θ) = cosθ

如图，可知sin(-θ)=-y=-sinθ，cos(-θ)=x=cosθ。

2.4 sin(90°+θ) = cosθ 、cos(90°+θ)=-sinθ

如图，根据三角函数的定义sin(90°+θ)=y’，cos(90°+θ)=x’。
又△B‘y’o全等于△BxO，有y’=x，x’=-y。
于是sin(90°+θ)=y’=x=cosθ，cos(90°+θ)=x’=-y=sinθ。
同理可得sin(180°+θ) = -sinθ，cos(180°+θ) = -cosθ。

2.5 余弦定理

余弦定理主要用来解答三角形中已知两边长度及其夹角，求第三边的长度的问题。

如图，已知AB、AC的长分别为c、b，及AB、AC的夹角为θ，求BC的长度a为多少？
公式为：a² = c²+b²-2bccosθ。
解法如下：
过B点做AC的垂线BD。

2.6 正弦定理

如图，已知△ABC外接圆的半径为r，则有a=2rsin∠A，b=2rsin∠B，c=2rsin∠C。

推导过程如下：
如图，设O为外接圆的圆心，则△AOB、△BOC、△AOC均为等腰三角形。
所以，∠A+∠B+∠C = （β+θ) + (β+γ) + (γ+θ) =2(β+θ+γ)= 180°
即β+θ+γ = 90°。
做辅助线OD垂直AC与点D。

可知AD = b/2。
则有

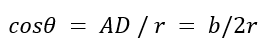
又

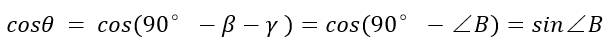
故

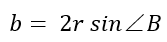
同理可得

2.7 cos⁡(θ-β) = cosθcosβ + sinθsinβ

此公式推导过程如下：

△OBB’中，根据余弦定理有

又有

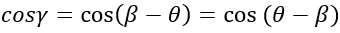
故

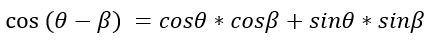
利用上面这个公式，咱们还可以推导出其他公式。
比如，我们设β = 90°-α，代入上面公式，则有

即

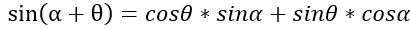
3 三角函数图像性质

4 Unity中三角函数常用到的地方

上面说了这么多，三角函数到底有什么用？
①在Unity中，只要涉及到旋转和角度，就不可避免的要用到三角函数，比如不同坐标系的变换矩阵、向量的点积和叉积等
②sin和cos函数是周期波动的，我们可以用这个性质来模拟旗帜的飘动和水的波动
③任何信号经过傅里叶变换都可以分解为无数正余弦信号的叠加，我们可以通过这些正余弦信号的频率和幅值得出一些有意义的信息，比如图片中是否有噪声
④欧拉公式

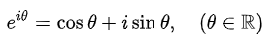
博主个人博客本文链接。