最小二乘法多元函数超曲面拟合问题

网上很多用最小二乘法拟合曲面的问题，但是最后给的例子都是拟合高维平面，本篇文章简单介绍用最小二乘法进行曲面拟合的方法，以二元函数的曲面逼近为例，用python实现，代码在文章最后。

一、最小二乘法

首先还是对最小二乘法的原理进行简单介绍：
考虑模型：

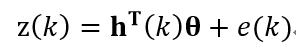
的辨识问题，式中z(k)和h(k）都是可观测数据，θ是待估参数，取准则函数：

极小化J(θ),求得θ的估计值，将使模型的输出最好的预报系统的输出。
将上式对θ求导，然后使导数等于零的时候取得的θ值即为参数矩阵的最优解，本篇文章中从头至尾忽略噪声项e(k)。推导过程我就不写了这个到处都是，直接写结果，参数矩阵θ的最优解为：

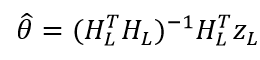
这里面要注意括号里必须是正则矩阵（即矩阵为非奇异，行列式的值不为0）

二、在拟合曲面时输入矩阵的选取

因为这篇文章是在二元函数的曲面方程拟合的情况下，多元的道理一样，自己去写参数多项式的项就可以了。
所以先假定两个输入值是x和y，z是函数的输出，如果z=ax + by, 就是一个最普通的平面，但是当扩展到一个二次曲面的时候，曲面的一般式就变成了z = ax^2 + by^2+cxy +dx +ey+f ,更高次的也是一样。本质上就是把原本只能用来解决线性问题的最小二乘法用来解决非线性问题，方法就是用多项式组合形式来替换输入值，让输出结果变成是各多项式线性组合的结果。

如图所示，在二元函数的情况下就不停地升高曲面的次数去逼近曲面，在每个次数下都要遍历各种可能的线性组合的多项式，上图中红色框里表示的是在升高次数之后已经含有的较低次数里的项，在编写生成多项式算法的时候就可以利用这个特性来简化算法的描述，这里显然就是利用递归来描述的。而最小二乘法拟合曲面时就是去得到各个多项式前面的参数，然后线性叠加各个项，那如果少掉某项的话当然也是可以的，只是会影响精度。最小二乘法的精髓就在于它会自己利用输入项里面的各种线性叠加来得到你想要的准确的估计值。下面就来写最关键的生成输入多项式的函数：

def Hl_matrix_generate(input_x,input_y,n):if n==0 :#判断初始情况，也就是在输入矩阵的最后填上一个常数项Hl_array = np.ones([144,1])#这里行数表示的是观测数据的总数，根据自己的情况改return Hl_arrayelif n > 0 :#判断n的值Hl_array = np.zeros([144, 1])#初始化矩阵数据for i in range(n+1):Hl_array = np.c_[Hl_array,(input_x**(n-i))*(input_y**i)]#生成在该阶次下更新的多项式的值，更新矩阵Hl_array = np.delete(Hl_array,0,axis= 1)#删掉第一列初始化的Hl_array = np.c_[Hl_array,Hl_matrix_generate(input_x,input_y,n-1)]#在该阶次下更新的多项式加上n-1次包含的多项式的值，完成递归return Hl_array

生成输入数据的函数和生成多项式的函数基本上是相同的，只不过输入只有一行，多项式函数里包含所有观测数据。输入函数如下：

def input_Func(input_x,input_y,n):if n==0 :Hl_array = np.ones([1,1])return Hl_arrayelif n > 0 :Hl_array = np.zeros([1, 1])for i in range(n+1):Hl_array = np.c_[Hl_array,(input_x**(n-i))*(input_y**i)]Hl_array = np.delete(Hl_array,0,axis= 1)Hl_array = np.c_[Hl_array,input_Func(input_x,input_y,n-1)]result = Hl_arrayreturn result

这个就不多解释了

然后就是生成估计参数矩阵，也就是刚刚的第三个公式：

#生成估计参数矩阵
def predicParamater_array_generate(input_paramater_array,output_paramater_array):predicPara_arr = (np.linalg.inv(np.mat(input_paramater_array).T * np.mat(input_paramater_array)))*np.mat(input_paramater_array).T*np.mat(output_paramater_array).Treturn predicPara_arr

最后输入乘上参数估计矩阵就得到了在该参数估计下的预测值，也是使得准则函数取值最小的估计值，更高次更多元的最小二乘法拟合大抵如此，在设计系统变化时也可以加进时间维度，可以根据这个方法举一反三，总之广义的最小二乘法是无敌的。

最后附上全部代码：

import numpy as np
np.set_printoptions(suppress=True)
np.set_printoptions(threshold=np.inf)#加载数据集函数
def loadDataSet():dataMat = []; labelMat = []fr = open('database_2D.txt')for line in fr.readlines():lineArr = line.strip().split()dataMat.append([float(lineArr[0]),float(lineArr[1])])labelMat.append([float(lineArr[2]),float(lineArr[3]),float(lineArr[4]),float(lineArr[5]),float(lineArr[6]),float(lineArr[7]),float(lineArr[8]),float(lineArr[9]),float(lineArr[10]),float(lineArr[11]),float(lineArr[12]),float(lineArr[13])])return dataMat,labelMat#生成输入矩阵函数
def Hl_matrix_generate(input_x,input_y,n):if n==0 :Hl_array = np.ones([144,1])return Hl_arrayelif n > 0 :Hl_array = np.zeros([144, 1])for i in range(n+1):Hl_array = np.c_[Hl_array,(input_x**(n-i))*(input_y**i)]Hl_array = np.delete(Hl_array,0,axis= 1)Hl_array = np.c_[Hl_array,Hl_matrix_generate(input_x,input_y,n-1)]return Hl_array#生成估计参数矩阵
def predicParamater_array_generate(input_paramater_array,output_paramater_array):predicPara_arr = (np.linalg.inv(np.mat(input_paramater_array).T * np.mat(input_paramater_array)))*np.mat(input_paramater_array).T*np.mat(output_paramater_array).Treturn predicPara_arr#生成数据预测函数
def input_Func(input_x,input_y,n):if n==0 :Hl_array = np.ones([1,1])return Hl_arrayelif n > 0 :Hl_array = np.zeros([1, 1])for i in range(n+1):Hl_array = np.c_[Hl_array,(input_x**(n-i))*(input_y**i)]Hl_array = np.delete(Hl_array,0,axis= 1)Hl_array = np.c_[Hl_array,input_Func(input_x,input_y,n-1)]result = Hl_arrayreturn result'''
********************************************
***             main code                ***
********************************************
'''
#参数设置  input_X  和 input_Y  是 两个输入角度 n 是最小二乘法阶数
input_x = 45
input_y = 135
n = 8 #阶#加载数据集
input_data , output_data = loadDataSet()#转换矩阵格式
input_data = np.array(input_data)
output_data = np.array(output_data)#生成输入数据矩阵
Hl_array = Hl_matrix_generate(input_data[:,0],input_data[:,1],n)
input_data = input_Func(input_x,input_y,n)
#print(Hl_array)for i in range(12):#生成参数矩阵predicParamater_arr = predicParamater_array_generate(Hl_array,output_data[:,i])#数据预测result = input_data*predicParamater_arrprint(result)