
全称:Karhunen–Loeve变换(卡洛南-洛伊变换)前面讨论的特征选择是在一定准则下,从n个特征中选出k个来反映原有模式。这种简单删掉某n-k个特征的做法并不十分理想,因为一般来说,原来的n个数据各自在不同程度上反映了识别对象的某些特征,简单地删去某些特征可能会丢失较多的有用信息。如果将原来的特征做正交变换,获得的每个数据都是原来n个数据的线性组合,然后从新的数据中选出少数几个,使其尽可能多地反映各类模式之间的差异,而这些特征间又尽可能相互独立,则比单纯的选择方法更灵活、更有效。K-L变换就是一种适用于任意概率密度函数的正交变换。
离散的有限K-L展开式的形式
设一连续的随机实函数x(t),
 (1)
(1)
式中,aj为展开式的随机系数,φj(t)为一连续的正交函数,它应满足:
其中

将上式写成离散的正交函数形式,使连续随机函数x(t)和连续正交函数φj(t)在区间


写成向量形式:

将式(1)取n项近似,并写成离散展开式:

其中,a为展开式中随机系数的向量形式,即:
a = (a1, a2, …, aj, …, an)T
其中,每一列为正交函数集中的一个函数,小括号内的序号为正交函数的采样点次序。因此,Φ实质上是由φj向量组成的正交变换矩阵,它将x变换成a。
如果对c种模式类别{
wi
}i=1,…,c做离散正交展开,则对每一模式可分别写成:xi=
Φai,其中矩阵
Φ取决于所选用的正交函数。对各个模式类别,正交函数都是相同的,但其展开系数向量ai则因类别的不同模式分布而异。K-L展开式的根本性质是将随机向量x展开为另一组正交向量wj的线性和,且其展开式系数aj(即系数向量a的各个分量)具有不同的性质。
正交向量集{φj}的确定
设随机向量x的总体自相关矩阵为R = E{xxT}。由

将x=Φa代入R = E{xxT},得:
要求系数向量a的各个不同分量应统计独立,即应使(a1, a2, …, aj, …, an)满足如下关系:
写成矩阵形式,应使:E{a aT} = Dλ,其中Dλ为对角形矩阵,其互相关成分均为0,即:

则:
由于Φ中的各个向量φj都相互归一正交,故有:
其中,φj向量对应为:
Rφj=λjφj
可以看出,λj是x的自相关矩阵R的特征值,φj是对应的特征向量。因为R是实对称矩阵,其不同特征值对应的特征向量应正交,即:
由式(1),K-L展开式系数应为:
K-L展开式用于特征选择相当于一种线性变换。若从n个特征向量中取出m个组成变换矩阵φ,即
φ = (φ1 φ2 … φm),m<n
此时,φ是一个n*m维矩阵,x是n维向量,经过φTx变换,即得到降维为m的新向量。
从K-L展开式的性质和按最小均方差的准则来选择特征,应使E[aj]=0。由于E[a]=E[φ Tx]= φ TE[x],故应使E[x]=0。基于这一条件,在将整体模式进行K-L变换之前,应先将其均值作为新坐标轴的原点,采用协方差矩阵C或自相关矩阵R来计算特征值。如果E[x] ≠0,则只能得到“次最佳”的结果。将K-L展开式系数aj(亦即变换后的特征)用yj表示,写成向量形式:y= φ Tx。此时变换矩阵φ 用m个特征向量组成。为使误差最小,不采用的特征向量,其对应的特征值应尽可能小。因此,将特征值按大小次序标号,即
λ1>λ2>…> λm>…> λn>=0
若首先采用前面的m个特征向量,便可使变换误差最小。K-L变换是在均方误差最小的意义下获得数据压缩(降维)的最佳变换,且不受模式分布的限制。对于一种类别的模式特征提取,它不存在特征分类问题,只是实现用低维的m个特征来表示原来高维的n个特征,使其误差最小,亦即使其整个模式分布结构尽可能保持不变。通过K-L变换能获得互不相关的新特征。若采用较大特征值对应的特征向量组成变换矩阵,则能对应地保留原模式中方差最大的特征成分,所以K-L变换起到了减小相关性、突出差异性的效果。在此情况下, K-L变换也称为主成分变换(PCA变换)。
需要指出的是,采用K-L变换作为模式分类的特征提取时,要特别注意保留不同类别的模式分类鉴别信息,仅单纯考虑尽可能代表原来模式的主成分,有时并不一定有利于分类的鉴别。
K-L变换实例
给定两类模式,其分布如图所示,试用K-L变换实现一维的特征提取(假定两类模式出现的概率相等)。
符合K-L变换进行特征压缩的最佳条件。
因P(ω1)= P(ω2)=0.5,故
解特征值方程|R-λI|=0,求R的特征值。
由(25.4-λ)2 – 25.02 = 0,得特征值λ1=50.4,λ2=0.4
其对应的特征向量可由RФi=λiФi求得:

选λ1对应的变换向量作为变换矩阵,由y=ФTx得变换后的一维模式特征为:





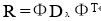

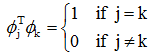





 支付宝扫一扫
支付宝扫一扫 微信扫一扫
微信扫一扫












.png)

.png)
