（一）重极限（多元函数的极限）

 

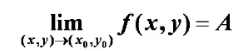
要掌握简单求重极限的方法，在判断连续性，特别是判断可微性时会用到。

高数 | 【多元函数微分学】多元函数求极限方法总结_西皮呦的博客-CSDN博客_多元函数求极限的方法总结

注：

---

（二）连续

1）定义

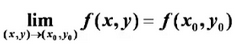
多元函数无间断点的分类，因为花样太多。

2）性质

多元函数也有零点定理，因为用的太少，这里不给出。

考点：会用定义判断多元函数在该点的连续性。

---

（三）偏导数

注：

       这里是偏增量，全微分才用到全增量。

★★★ 偏导数 本质上 就是 一元函数的导数。

      

★★★ 故求多元函数偏导，可以先代后求，也可以用定义。如：

 

 ★★★ 求分界点、不连续点处或者求出偏导函数后无法代入某点时，则需要用定义求偏导数。

 

---

 （四）全微分、可微

 全微分与全增量：

 可微：

 

注：函数不一定是在任何一点偏导数连续，故函数可微推不出偏导数各点连续。

可微的几何意义

---

（五）连续、可偏导及可微之间的关系

 

 注：偏导连续默认指一阶偏导连续

多元函数与一元函数的区别就在 第一张图的蓝色框框。

而这一切的一切都是因为偏导引起的。为什么呢？

 

偏导实际上就是固定x或固定y，一条线上的导数。偏导只与这两条线上的函数值有关。

而连续要求任意方向趋向某点的极限都…

可微就更不肯能了，可微要求的是全增量，你偏导就给我一个方向的增量，我不干。

 注：

• 一元函数
• 一元函数连续不一定可导，连续不一定可微： |x|
• 一元函数可微与可导互为充要条件证明：高数 | 一元可微与可导(互为充要条件证明)_西皮呦的博客-CSDN博客_一元函数可微的证明
• 一元函数的可导与可微等价，可通俗的认为二者均表示曲线连续且光滑，且切线无竖直情况。

• 多元函数经典反例
• 多元函数可导不一定连续：
• 
•  多元函数可导不一定可微：
• 
• 可微一定可偏导，反之不成立：两个线属性存在，并不能推出一个可微的面属性！
• 可微是一个曲面点处的切平面存在且不可垂直于xoy 平面，可导是一个曲面点处沿着x,y轴的切线存在。所以有切面一定有切线，但是切线不一定连成切面。所以可微一定可导。可导不一定可微。
• 

• 二元函数f在其定义域内某点是否连续与偏导数是否存在无关。

• 判断可导、可微、连续的注意事项：
• 1、在一元的情况下，可导=可微->连续，可导一定连续，反之不一定。
• 2、二元就不满足以上的结论，在二元的情况下：
• （1）偏导数存在且连续，函数可微，函数连续。
• （2）偏导数不存在，函数不可微，函数不一定连续。
• （3）函数不可微，偏导数不一定存在，函数不一定连续。
• （4）函数连续，偏导数不一定存在,函数不一定可微。
• （5）函数不连续，偏导数不一定存在,函数不可微。

---

题型： 讨论连续性、 可导性、 可微性

 

 

 D

A、连续   B、可导   D、x和y都要趋向

 

 

回顾四个等价形式。

---

参考文章：

kaysen学长：二元微分，连续、可微、可偏导、偏导连续的超强通俗解析！ – 知乎
为什么偏导数连续，函数就可微？_马同学图解数学的博客-CSDN博客_偏导数连续为什么一定可微

这篇文章写得也忒好了 ！！给哥哥倒一杯卡布奇诺 ~