Lyapunov稳定性分析2（连续时间系统）

    • 一、李雅普诺夫第一方法（==间接法==）
    • 二、李雅普诺夫第二方法（==直接法==）
    • 三、李雅普诺夫稳定性判定（连续时间系统）
      • 3.1 Lyapunov渐近稳定的充要条件（==第一方法==）：
      • 3.2 举例：MATLAB判断系统稳定性（==Lyapunov第一方法==）
      • 3.3 Lyapunov渐近稳定的充要条件（==第二方法==）
      • 3.4 举例：MATLAB判断系统稳定性（==Lyapunov第二方法==）
          • （1）**==MATLAB函数形式：==**
          • （2） **==Example1==**：MATLAB自带的例子
          • （3） **==Example2==**：
          • （4） **==Example3==**：

**注：**Lyapunov稳定性理论主要内容：
李雅普诺夫第一方法和
第二方法，本篇文章只分析
线性系统稳定性，
非线性系统稳定性将单独写文章进行分析！敬请关注，谢谢~

一、李雅普诺夫第一方法（间接法）

线性系统，只须求出系数矩阵的特征值即可判断其稳定性（见作者”控制系统分析1（线性系统稳定性和收敛性）”博客）；
非线性系统，则由若干过程组成，其中每个过程都要用到具体的形式。由系统的动态方程来找出其一次近似的线性化方程，在通过对线性化方程的稳定性的分析而给出原非线性系统在小范围内稳定性的有关信息。

二、李雅普诺夫第二方法（直接法）

李雅普诺夫第二方法：又称直接法， 不需要引入线性近似，而直接由系统的运动方程出发，通过构造一个类似于能量的Lyapunov函数，并分析它和其一次导数的定号性而获得系统稳定性的有关信息
　　能量函数：状态和时间的标量函数，又称为李雅普诺夫函数，记作V(x,t)。

三、李雅普诺夫稳定性判定（连续时间系统）

3.1 Lyapunov渐近稳定的充要条件（第一方法）：

定理：
某一线性时不变系统：
　　Lyapunov稳定性分析2（连续时间系统）-编程知识网
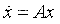
　　如果系统矩阵A的特征值全部在左半平面，即特征值都小于0，即A的所有特征值都具有负实部，则系统的平衡状态 xe 是渐近稳定的。

3.2 举例：MATLAB判断系统稳定性（Lyapunov第一方法）

A=[-3 -6 -2 -1;1 0 0 0;0 1 0 0;0 0 1 0];
B=[1;0;0;0];C=[0 0 1 1];D=[0]; %系统状态方程
flag=0;  %设定标志变量，判断系统是否稳定
[z,p,k]=ss2zp(A,B,C,D,1);
disp('系统零点、极点和增益分别为：');
z
p
k
for i=1:length(A)  %判断是否稳定if real(p(i)) > 0flag = 1;end
end
%显示结果
if flag == 1disp('系统不稳定');
elsedisp('系统稳定');
end

得到：

系统零点、极点和增益分别为：z =-1p =-1.3544 + 1.7825i-1.3544 - 1.7825i-0.1456 + 0.4223i-0.1456 - 0.4223ik =1系统稳定

系统矩阵A的特征值实部均小于0，所以系统稳定。

3.3 Lyapunov渐近稳定的充要条件（第二方法）

定理：
某一线性时不变系统：
Lyapunov稳定性分析2（连续时间系统）-编程知识网
A为n×n常数非奇异矩阵，对于任意的正定矩阵Q，系统在平衡状态x=0处是大范围渐近稳定的充分必要条件是：存在一个正定的实对称阵P，满足李雅普诺夫(矩阵代数)方程：
Lyapunov稳定性分析2（连续时间系统）-编程知识网
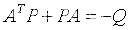
先设定Lyapunov函数，再得到Lyapunov方程，最后去分析稳定性
Lyapunov稳定性分析2（连续时间系统）-编程知识网
标量函数 V(x) = xTPx 就是系统的李雅普诺夫函数

3.4 举例：MATLAB判断系统稳定性（Lyapunov第二方法）

（1）MATLAB函数形式：

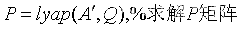
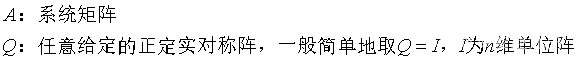
Lyapunov稳定性分析2（连续时间系统）-编程知识网
Lyapunov稳定性分析2（连续时间系统）-编程知识网
注意：
①. 这里只求解开环系统稳定性，只分析系统矩阵A，还没有涉及到闭环系统反馈矩阵K以及闭环状态状态矩阵Acl=(A–BK)，
②. 这里的Q只是任意给定的正定实对称阵，用来求解正定实对称阵P，再判断P是否正定，从而确定开环系统是否稳定，一般可取为单位阵I，不同于LQR中的状态2范数的权值矩阵Q。
③. 只要矩阵Q选成是正定的（或在许可时选为半正定的），那么对系统渐近稳定的最终结果与Q 的具体选取无关。

（2） Example1：MATLAB自带的例子

Lyapunov稳定性分析2（连续时间系统）-编程知识网
注：这里的Lyapunov方程是AX+XAT+Q=0，A已经是系统矩阵的转置了，所以lyap()函数里不用再转置。
①. 很明显求出的实对称阵X(即为P)一阶、二阶顺序主子式行列式均大于0，说明求解的对称矩阵P是正定的，所以系统稳定。
②. 再用Lyapunov第一方法验证：系统矩阵A的特征值均小于0，所以该系统稳定，Lyapunov方程有解。
Lyapunov稳定性分析2（连续时间系统）-编程知识网

（3） Example2：

Lyapunov稳定性分析2（连续时间系统）-编程知识网
①. 系统Lyapunov方程无解。
②. 再用Lyapunov第一方法验证：系统矩阵A存在一个特征值大于0，所以该系统不稳定，Lyapunov方程无解。

（4） Example3：
A=[1 -3.5 4.5;2 -4.5 4.5;-1 1.5 -2.5];
B=[-0.5;-0.5;-0.5]';C=[1 0 1]; %系统状态方程
Q=eye(3,3);  %Q=I
P=lyap(A,Q); %求解矩阵P
%显示矩阵P的各阶主子式的值并判断是否稳定
flag=0;
disp('矩阵P的各阶主子式的值分别为：');
for i=1:length(A)  %判断是否稳定det(P(1:i,1:i))if real(P(i)) > 0flag = 1;end
end
if flag == 1disp('系统稳定');
elsedisp('系统不稳定');
end

得到：

矩阵P的各阶主子式的值分别为：ans =1.4825ans =0.6725ans =0.1169系统稳定

①. 求解出来的矩阵P各阶主子式均大于0，说明求解的对称矩阵P是正定的，所以系统稳定

   P=lyap(A,Q); %求解矩阵P
>> PP =1.4825    0.5825    0.01250.5825    0.6825    0.31250.0125    0.3125    0.3825>> det(P(1:1,1:1))ans =1.4825>> det(P(1:2,1:2))ans =0.6725>> det(P(1:3,1:3))ans =0.1169

②. 同样用Lyapunov第一方法验证：系统矩阵A的特征值均小于0，所以该系统稳定，Lyapunov方程有解。

eig([1 -3.5 4.5;2 -4.5 4.5;-1 1.5 -2.5])ans =-4.0000-1.0000-1.0000