
今天来学习一个新的东西—指数循环节。在有些题目中我们需要对指数进行降幂处理才能计算。比如计算
其中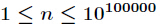
这里由于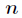
有了上述公式,很多题目就可以迎刃而解了。
题目:http://acm.fzu.edu.cn/problem.php?pid=1759
题意:给定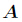
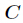
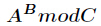
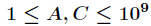
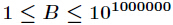
代码:
#include <iostream>
#include <string.h>
#include <stdio.h>using namespace std;
const int N=1000005;
typedef long long LL;char str[N];int phi(int n)
{int rea = n;for(int i=2; i*i<=n; i++){if(n % i == 0){rea = rea - rea / i;while(n % i == 0) n /= i;}}if(n > 1)rea = rea - rea / n;return rea;
}LL multi(LL a,LL b,LL m)
{LL ans = 0;a %= m;while(b){if(b & 1){ans = (ans + a) % m;b--;}b >>= 1;a = (a + a) % m;}return ans;
}LL quick_mod(LL a,LL b,LL m)
{LL ans = 1;a %= m;while(b){if(b & 1){ans = multi(ans,a,m);b--;}b >>= 1;a = multi(a,a,m);}return ans;
}void Solve(LL a,char str[],LL c)
{LL len = strlen(str);LL ans = 0;LL p = phi(c);if(len <= 15){for(int i=0; i<len; i++)ans = ans * 10 + str[i] - '0';}else{for(int i=0; i<len; i++){ans = ans * 10 + str[i] - '0';ans %= p;}ans += p;}printf("%I64d\n",quick_mod(a,ans,c));
}int main()
{LL a,c;while(~scanf("%I64d%s%I64d",&a,str,&c))Solve(a,str,c);return 0;
}
题目:http://acm.hdu.edu.cn/showproblem.php?pid=2837
题意:给定一个递归式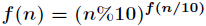

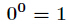
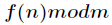
分析:本题方法比较明确,先已一直递归上去,直到
数降幂,这里需要判断。
代码:
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <math.h>using namespace std;
typedef long long LL;int phi(int n)
{int rea = n;for(int i=2; i*i<=n; i++){if(n % i == 0){rea = rea - rea / i;while(n % i == 0) n /= i;}}if(n > 1)rea = rea - rea / n;return rea;
}LL quick_mod(LL a,LL b,LL m)
{LL ans = 1;a %= m;while(b){if(b & 1){ans = ans * a % m;b--;}b >>= 1;a = a * a % m;}return ans;
}LL check(LL a,LL b,LL p)
{LL ans = 1;for(int i=1; i<=b; i++){ans *= a;if(ans >= p)return ans;}return ans;
}LL dfs(LL n,LL m)
{LL p = phi(m);if(n < 10) return n;LL x = dfs(n / 10, p);LL y = check(n % 10, x, m);if(y >= m){LL ans = quick_mod(n % 10, x + p, m);if(ans == 0)ans += m;return ans;}elsereturn y;
}int main()
{int T;cin>>T;while(T--){LL n,m;cin>>n>>m;cout<<dfs(n,m) % m<<endl;}return 0;
}
题目:http://acm.nefu.edu.cn/JudgeOnline/problemshow.php?problem_id=691
题意:给定一个数组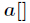
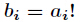
分析:方法基本跟上题一样,就不多说了。注意特殊处理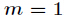
代码:
#include <iostream>
#include <string.h>
#include <stdio.h>using namespace std;
typedef long long LL;
const int N = 105;LL a[N],p[N];LL phi(LL n)
{LL rea = n;for(int i=2; i*i<=n; i++){if(n % i == 0){rea = rea - rea / i;while(n % i == 0) n /= i;}}if(n > 1)rea = rea - rea / n;return rea;
}void Init(LL m)
{p[0] = m;for(int i=1; i<N; i++)p[i] = phi(p[i-1]);
}LL Solve(int dept,bool &f)
{LL m = p[dept];if(m == 1){if(a[dept] > 1) f = 1;else f = 0;return 0;}if(a[dept] >= m){f = 1;return 0;}LL t = 1;bool flag = 0;for(int i=1;i<=a[dept];i++){t = t * i;if(t >= p[dept]){flag = 1;t %= m;}}LL d = Solve(dept+1,f);if(f) d += phi(m);LL ans = 1;f = 0;for(int i=0;i<d;i++){ans = ans * t;if(ans >= m){f = 1;ans %= m;}if(flag) f = 1;}return ans;
}int main()
{int T;cin>>T;while(T--){LL n,m;cin>>n>>m;for(int i=0; i<n; i++)cin>>a[i];if(m == 1){puts("0");continue;}Init(m);bool f;cout<<Solve(0,f)<<endl;}return 0;
}
题目:http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=1674
题意:已知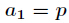
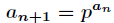
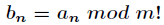
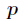
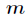
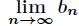
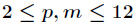
分析:本题方法很巧妙,由于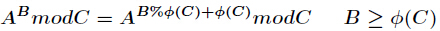
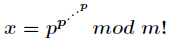
那么有
可以看出

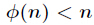
代码:
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <math.h>using namespace std;
typedef long long LL;LL phi(LL n)
{LL rea = n;LL t = (LL)sqrt(1.0*n);for(int i=2;i<=t;i++){if(n % i == 0){rea = rea - rea / i;while(n % i == 0) n /= i;}}if(n > 1)rea = rea - rea / n;return rea;
}LL power(LL a,LL b,LL m)
{LL ans = 1;a %= m;while(b){if(b & 1){ans = ans * a % m;b--;}b >>= 1;a = a * a % m;}return ans;
}LL Solve(LL a,LL m)
{if(m == 1) return 0;LL p = phi(m);return power(a,p,m) * power(a,Solve(a,p),m) % m;
}int main()
{LL a,m;bool f = 1;while(cin>>a>>m){if(f) f = 0;else puts("");LL ans = 1;for(int i=1;i<=m;i++)ans *= i;cout<<Solve(a,ans)%ans<<endl;}return 0;
}
题目:http://acm.hdu.edu.cn/showproblem.php?pid=4335
题意:给定3个整数
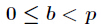
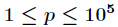
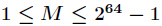
的个数。
分析:由
代码:
#include <iostream>
#include <string.h>
#include <stdio.h>using namespace std;
typedef unsigned long long ULL;int phi(int n)
{int rea = n;for(int i=2; i*i<=n; i++){if(n % i == 0){rea = rea - rea / i;while(n % i == 0) n /= i;}}if(n > 1)rea = rea - rea / n;return rea;
}ULL quick_mod(ULL a,ULL b,ULL m)
{ULL ans = 1;a %= m;while(b){if(b & 1){ans = ans * a % m;b--;}b >>= 1;a = a * a % m;}return ans;
}ULL f[100005];int main()
{int T;scanf("%d", &T);for(int t=1; t<=T; t++){ULL b, p, m;scanf("%I64u %I64u %I64u", &b, &p, &m);if(b == 0 && p == 1 && m == 18446744073709551615ull){printf("Case #%d: 18446744073709551616\n",t);continue;}int ph = phi(p);ULL ans = 0;if(b == 0) ans++;f[0] = 1;bool flag = 0;int i;for(i=1; i<=m; i++){f[i] = f[i-1] * i;if(f[i] >= ph){f[i] %= ph;flag = 1;if(f[i] == 0) break;}if(flag){if(quick_mod(i, f[i] + ph, p) == b)ans++;}else{if(quick_mod(i, f[i], p) == b)ans++;}}for(int k=0; i<=m && k<p; i++, k++)if(quick_mod(i, ph, p) == b)ans += 1 + (m - i) / p;printf("Case #%d: %I64u\n", t, ans);}return 0;
}

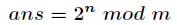
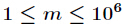
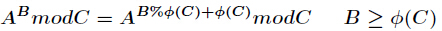

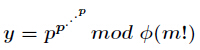
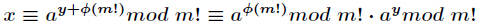

 支付宝扫一扫
支付宝扫一扫 微信扫一扫
微信扫一扫












.png)

.png)
