1、LDA线性判别分析  

http://blog.csdn.net/raby_gyl/article/details/20362373

也称FLD（Fisher线性判别）是一种有监督的学习方法（supervised learning）。

LDA的基本思想是：

找到一个最佳的判别矢量空间，使得投影到该空间的样本的类间离散度与类内离散度比达到最大。

LDA的目的：

是从高维空间中提取出最优判别力的低维特征，这些特征使同一类别的样本尽可能的靠近，同时使不同类别的样本尽可能的分开，即选择使样本的类间散布矩阵和类内散布矩阵达到最大比值的特征。因此，用FLD得到的特征不但能够较好的表示原始数据，而且更适合分类。

LDA的两个基本用途：

降维和分类器（例如OpenCV中将LDA和K邻近分类器封装为一个“分类器”，这里K=1。所以本质还是降维和使数据易于可分）

LDA降维思想：

1）训练模型

数据(D):高维特征矢量

训练(T):操作模式

规则(R):训练数据的规则

黑盒子(B):如果我们只是想应用而不想理解其内部的复杂原理，我们可以不关系黑盒子里面是如何操作的。

模型(M):训练的结果，即产生(P)一个模型，这里是上面描述的一个矢量空间。

2）将高维数据送入模型实现降维

LDA分类器思想：

这里的分类思想，是OpenCV一种封装的分类思想，OpenCV在人脸识别算法中将LDA+1—邻近分类器组合，构造所谓的“合成分类器”，相当于类中的封装。

1）将所有训练样本图像投影到LDA子空间

2）将测试图像投影到LDA子空间

3）找到投影后的训练样本集和测试图像之间的最邻近，即如果测试图像与训练样本中的b最邻近，b属于C类，那么测试图像也属于C类。

LDA原理和计算过程：

LDA是一种线性分类器，它可以看作是SVM的简化版本。

正因为它是一种线性分类器，所以对于K-分类问题，有K-1个线性函数：

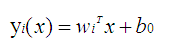
这个线性函数就是一个分类器。x是输出矢量，w是权重，y为输出值。对于两类，我们设置一个阈值y0,如果对于某些矢量x，带入到线性函数中的输出值y大与y0,则为一类，小于y0则为另一类。其实可以理解为：对于输入矢量x，这些矢量在一个多维 矢量空间中分布，wk就是一个权重，或者认为一个矢量空间，也或者认为是一个方向矢量，我们将x投影到矢量空间，或者说沿着这个方向上的投影后的值变为y,每一个矢量x对应投影后的一个值，对于不同的类别有不同的y值，或者y值范围，这使得数据变的更加容易可分。

注：关于类间离散度矩阵Sb的秩的参考理解（不是推导）：

例如：

对于二维点集的二分类问题。由于是二分类问题，那么上述公式3-36变为Wfld={W1}，p为1。那么利用公式3-37后的，y表示矢量x在w1方向的投影坐标。此时y数据的分布变的更加容易可分。

换角度理解：

我们知道Wlfd={w1,w2,w3,…,wp}，其中p<=C-1；

我们知道对于C类，如果用线性分类器进行分类的话，需要C-1个分类器。如对于两类，我们只需要一个分类函数，从中间劈开。

我们组合下面两个公式进行理解：

上述第一个公式表示为一个线性分类器，第二个公式表示p个线性分类器（这里的p取C-1)。

一个分类器可以对二类问题进行分类，那么第一个公式表示待分类矢量x经过投影变化后得到的y值更加容易可分。

p个分类器可以对p+1（即C）类问题进行分类，那么第二个公式表示待分类矢量x经过投影变化后得到矢量y更加容易可分。

应用降维思路：

训练数据的处理：

1、循环读入训练图像Mat，并将Mat对象存储到vector<Mat>容器中，同时新建一个Mat对象，或行矢量或列矢量来存储类别标签。

2、将步骤1中的数据传入到LDA的构造函数中，构造函数进行计算处理，从而获得特征矢量。

3、将训练数据利用project函数，投影到特征矢量构造的子空间，即LDA子空间，将返回的Mat矢量保存起来，做后续的处理。

4、将LDA对象，利用save保存起来。

测试数据的处理：

1、利用load函数将LDA导入

2、利用project函数，将测试数据投影到LDA子空间，保存返回的Mat矢量，做后续的处理。

LDA其他知识

转换矩阵W，可以将样本投影到c-1维空间，其中c表示类别。

PCA对光照的灵敏度将高。LDA对光照不如PCA对光照的敏感。LDA的性能同样严重的依赖于输入的数据。

LDA也可以像PCA那样对图像进行重建，但是LDA重建效果没有PCA好，这是因为PCA利用的个体的主成份特征，而LDA利用了辨别个体之间不同的特征。

2、PCA——主成份分析

PCA又叫K-L变换，是一个无监督的学习方法。

PCA和LDA类似这里不在书写，网上资料也一大把。只给出几个连接：

1）PCA理论分析及应用

2）OpenCV PCA

3、PCA+LDA

Wfld表示LDA的特征矢量构成的，Wpca表示PCA的特征矢量构成的，u是PCA分析中所有样本的均值。z矢量的维数为类别数目-1.

4、应用：基于Gabor小波和PCA+FLD+最邻近分类的人脸表情识别