
1、相机内参数是与相机自身特性相关的参数,比如相机的焦距、像素大小等;
相机外参数是在世界坐标系中的参数,比如相机的位置、旋转方向等。
相机标定(或摄像机标定):
一句话就是世界坐标到像素坐标的映射,当然这个世界坐标是我们人为去定义的,标定就是已知标定控制点的世界坐标和像素坐标我们去解算这个映射关系,一旦这个关系解算出来了我们就可以由点的像素坐标去反推它的世界坐标,当然有了这个世界坐标,我们就可以进行测量等其他后续操作了~上述标定又被称作隐参数标定,因为它没有单独求出相机的内部参数,如相机焦虑,相机畸变系数等~一般来说如果你仅仅只是利用相机标定来进行一些比较简单的视觉测量的话,那么就没有必要单独标定出相机的内部参数了~至于相机内部参数如何解算,相关论文讲的很多~

在图像测量过程以及机器视觉应用中,为确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系,必须建立相机成像的几何模型,这些几何模型参数就是相机参数。在大多数条件下这些参数必须通过实验与计算才能得到,这个求解参数的过程就称之为相机标定(或摄像机标定)
相机标定的目的是确定相机的一些参数的值。通常,这些参数可以建立定标板确定的三维坐标系和相机图像坐标系的映射关系,换句话说,你可以用这些参数把一个三维空间中的点映射到图像空间,或者反过来。
相机需要标定的参数通常分为内参和外参两部分。外参确定了相机在某个三维空间中的位置和朝向,至于内参,可以说是相机内部的参数(这好像是废话…笑),我觉得需要引入一点光学的东西来更好地解释一下。现有的相机都至少包含一个光学镜头和一个光电传感器(CCD或CMOS)。
通过镜头,一个三维空间中的物体经常会被映射成一个倒立缩小的像(当然显微镜是放大的,不过常用的相机都是缩小的),被传感器感知到。
- 理想情况下,镜头的光轴(就是通过镜头中心垂直于传感器平面的直线)应该是穿过图像的正中间的,但是,实际由于安装精度的问题,总是存在误差,这种误差需要用内参来描述;
- 理想情况下,相机对x方向和y方向的尺寸的缩小比例是一样的,但实际上,镜头如果不是完美的圆,传感器上的像素如果不是完美的紧密排列的正方形,都可能会导致这两个方向的缩小比例不一致。内参中包含两个参数可以描述这两个方向的缩放比例,不仅可以将用像素数量来衡量的长度转换成三维空间中的用其它单位(比如米)来衡量的长度,也可以表示在x和y方向的尺度变换的不一致性;
- 理想情况下,镜头会将一个三维空间中的直线也映射成直线(即射影变换),但实际上,镜头无法这么完美,通过镜头映射之后,直线会变弯,所以需要相机的畸变参数来描述这种变形效果。
1.外参数矩阵。告诉你现实世界点(世界坐标)是怎样经过旋转和平移,然后落到另一个现实世界点(摄像机坐标)上。
2.内参数矩阵。告诉你上述那个点在1的基础上,是如何继续经过摄像机的镜头、并通过针孔成像和电子转化而成为像素点的。
3.畸变矩阵。告诉你为什么上面那个像素点并没有落在理论计算该落在的位置上,还tm产生了一定的偏移和变形!!!
2、摄像机内参、外参矩阵
在opencv的3D重建中(opencv中文网站中:照相机定标与三维场景重建),对摄像机的内参外参有讲解:
外参:摄像机的旋转平移属于外参,用于描述相机在静态场景下相机的运动,或者在相机固定时,运动物体的刚性运动。因此,在图像拼接或者三维重建中,就需要使用外参来求几幅图像之间的相对运动,从而将其注册到同一个坐标系下面来
内参:下面给出了内参矩阵,需要注意的是,真实的镜头还会有径向和切向畸变,而这些畸变是属于相机的内参的。
摄像机内参矩阵:
fx s x0K = 0 fy y00 0 1
- 1
- 2
- 3
- 4
- 1
- 2
- 3
- 4
其中,fx,fy为焦距,一般情况下,二者相等,x0、y0为主点坐标(相对于成像平面),s为坐标轴倾斜参数,理想情况下为0
摄像机外参矩阵:包括旋转矩阵和平移矩阵
旋转矩阵和平移矩阵共同描述了如何把点从世界坐标系转换到摄像机坐标系
旋转矩阵:描述了世界坐标系的坐标轴相对于摄像机坐标轴的方向
平移矩阵:描述了在摄像机坐标系下,空间原点的位置
例:
<leftCameraMatrix type_id="opencv-matrix">
<rows>3</rows>
<cols>3</cols>
<dt>d</dt>
<data>
7.3582167224957209e+002 0. 1.5950000000000000e+002
0. 7.3582167224957209e+002 1.1950000000000000e+002
0. 0. 1.
</data></leftCameraMatrix>
二、 一些疑问
Q1:标定时棋盘格的大小如何设定,对最后结果有没有影响?
A:当然有。在标定时,需要指定一个棋盘方格的长度,这个长度(一般以毫米为单位,如果需要更精确可以设为0.1毫米量级)与实际长度相同,标定得出的结果才能用于实际距离测量。一般如果尺寸设定准确的话,通过立体标定得出的Translation的向量的第一个分量Tx的绝对值就是左右摄像头的中心距。一般可以用这个来验证立体标定的准确度。比如我设定的棋盘格大小为270 (27mm)???,最终得出的Tx大小就是602.8 (60.28mm),相当精确。
Q2:通过立体标定得出的Tx符号为什么是负的?
A:这个其实我也不是很清楚。个人的解释是,立体标定得出的T向量指向是从右摄像头指向左摄像头(也就是Tx为负),而在OpenCV坐标系中,坐标的原点是在左摄像头的。因此,用作校准的时候,要把这个向量的三个分量符号都要换一下,最后求出的距离才会是正的。
但是这里还有一个问题,就是Learning OpenCV中Q的表达式,第四行第三列元素是-1/Tx,而在具体实践中,求出来的实际值是1/Tx。这里我和maxwellsdemon讨论下来的结果是,估计书上Q表达式里的这个负号就是为了抵消T向量的反方向所设的,但在实际写OpenCV代码的过程中,那位朋友却没有把这个负号加进去。(一家之言,求更详细的解释)
Q3:cvFindStereoCorrespondenceBM的输出结果好像不是以像素点为单位的视差?
A:在OpenCV2.0中,BM函数得出的结果是以16位符号数的形式的存储的,出于精度需要,所有的视差在输出时都扩大了16倍(2^4)。其具体代码表示如下:
dptr[y*dstep] = (short)(((ndisp – mind – 1 + mindisp)*256 + (d != 0 ? (p-n)*128/d : 0) + 15) >> 4);
可以看到,原始视差在左移8位(256)并且加上一个修正值之后又右移了4位,最终的结果就是左移4位
因此,在实际求距离时,cvReprojectTo3D出来的X/W,Y/W,Z/W都要乘以16 (也就是W除以16),才能得到正确的三维坐标信息
Q4:利用双摄像头进行测距的时候世界坐标的原点究竟在哪里?
A:世界坐标系的原点是左摄像头凸透镜的光心。
说起这个,就不得不提到针孔模型。如图3所示,针孔模型是凸透镜成像的一种简化模型。当物距足够远时(远大于两倍焦距),凸透镜成像可以看作是在焦距处的小孔成像。(ref: http://bak1.beareyes.com.cn/2/lib/200110/04/20011004006.htm)
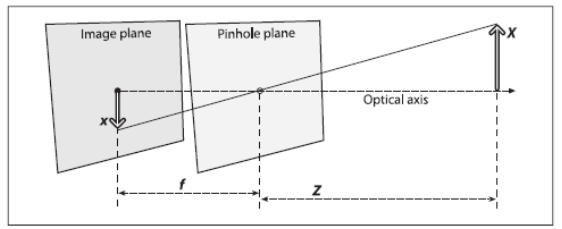
图3. 针孔模型
在实际计算过程中,为了计算方便,我们将像平面翻转平移到针孔前,从而得到一种数学上更为简单的等价形式(方便相似三角形的计算),如图4所示。
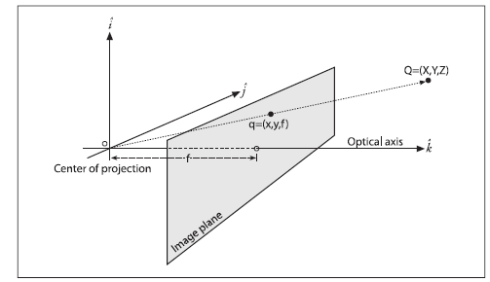
图4. 针孔模型的数学等价形式
因此,对应图2就可以知道,世界坐标系原点就是左摄像头针孔模型的针孔,也就是左摄像头凸透镜的光心
Q5:f和d的单位是像素,那这个像素到底表示什么,它与毫米之间又是怎样换算的?
A:这个问题也与针孔模型相关。在针孔模型中,光线穿过针孔(也就是凸透镜中心)在焦距处上成像,因此,图3的像平面就是摄像头的CCD传感器的表面。每个CCD传感器都有一定的尺寸,也有一定的分辨率,这个就确定了毫米与像素点之间的转换关系。举个例子,CCD的尺寸是8mm X 6mm,分辨率是640X480,那么毫米与像素点之间的转换关系就是80pixel/mm。
在实际运用中,我们在数学上将这个像平面等效到小孔前(图4),这样就相当于将在透镜中心点之前假设了一块虚拟的CCD传感器。
Q6:为什么cvStereoRectify求出的Q矩阵cx, cy, f都与原来的不同?
A:这个在前文有提到过。在实际测量中,由于摄像头摆放的关系,左右摄像头的f, cx, cy都是不相同的。而为了使左右视图达到完全平行对准的理想形式从而达到数学上运算的方便,立体 校准所做的工作事实上就是在左右像重合区域最大的情况下,让两个摄像头光轴的前向平行,并且让左右摄像头的f, cx, cy相同。因此,Q矩阵中的值与两个instrinsic矩阵的值不一样就可以理解了。

 支付宝扫一扫
支付宝扫一扫 微信扫一扫
微信扫一扫



.png)
.png)
.png)

.png)

