
码字总结不易,老铁们来个三连:点赞、关注、评论
作者:[左手の明天]
原创不易,转载请联系作者并注明出处
版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。
现实世界的变化受着众多因素的影响,包括确定的和随机的。如果从建模的背景、目的和手段看,主要因素是确定的,随机因素可以忽略,或者随机因素的影响可以简单地以平均值的作用出现,那么就能够建立确定性模型。如果随机因素对研究对象的影响必须考虑,就应建立随机模型。
讨论如何用随机变量和概率分布描述随机因素的影响,建立随机模型——概率模型
随机模型-确定性因素和随机性因素
确定性模型
研究的对象通常包含随机因素,但是如果从建模的背景、目的和手段看,主要因素是确定的,而随机因素可以忽略,或者随机因素的影响可以简单地以平均值的作用出现,那么就能够建立确定性模型。
随机性模型
随机因素对研究对象的影响必须考虑,就应该建立随机性模型。
目录
概率论基本知识
1、古典概型
2、随机变量及其分布
3、数学期望的概念和计算
4、MATLAB中相关的的概率命令
概率模型的典型案例
传送系统的效率
背景
模型分析
模型假设
模型建立
模型解释
模型评注
报童的诀窍
问题提出
模型分析
模型假设
模型建立
模型求解
结果解释
模型评注
模型应用
随机存贮策略
问题提出
模型假设
模型分析
模型建立
模型求解
模型评注
轧钢中的浪费
问题提出
模型假设
模型分析
模型建立
模型求解
模型应用
随机人口模型
问题提出
模型假设
模型建立
模型求解
模型评注
看这看这
概率论基本知识
1、古典概型
条件概率:在事件B发生的条件下,事件A发生的概率
例:现有100个零件,其中95个长度合格,94个直径和格,92个两个尺寸都合格。任取一个,发现长度合格,问直径合格的概率。
设A=‘长度合格’,B=‘直径合格’
全概率公式和贝叶斯公式
设B1,B2,…,Bn为样本空间S的一个划分,且有P(Bi)>0, i=1,2,…,n,则对E的任一事件A,有:
例:某电子设备制造厂所用的某种晶体管是由三家元件制造厂提供的,根据以往的记录有以下的数据:
设这三家的产品在仓库中是均匀混合的,且无区别的标志。现在仓库中随机地抽取一只晶体管,
(1)求它是次品的概率;
(2)若已知取到的是次品,问此次品是哪个厂生产的可能性更大?
2、随机变量及其分布
二项分布

贝努利试验
设随机试验E只有两种可能的结果:A及,且 P(A)=p,(0<p<1), 将试验E独立地重复进行n次, 简称n重贝努利试验(Bernoulli)。 n重贝努利试验中事件A出现的次数服从二项分布
泊松分布
n重贝努利试验中小概率事件出现的次数近似地服从泊松分布.
指数分布
背景:指数分布常用于可靠性统计研究中,如元件的寿命,动物的寿命,电话问题中的通话时间,服务时间等。
正态分布
背景:如果决定试验结果X的是大量随机因素的总和,假设各个因素之间近似独立,并且每个因素的单独作用相对均匀地小,那么X的分布近似正态分布。
3、数学期望的概念和计算
描述了随机变量的概率取值中心—均值
4、MATLAB中相关的的概率命令
MATLAB工具箱对每一种分布都提供5类函数,其命令字符为:
概率密度:pdf
概率分布:cdf
逆概率分布:inv
均值与方差:stat
随机数生成:rnd
当需要一种分布的某一类函数时,将以上所列的分布命令字符与函数命令字符接起来,并输入自变量(可以是标量、数组或矩阵)和参数即可.
如对均值为mu、标准差为sigma的正态分布,举例如下:
- 1.密度函数:p=normpdf(x,mu,sigma) (当mu=0,sigma=1时可缺省)
在MATLAB中输入以下命令:
x=-6:0.01:6;
y=normpdf(x); z=normpdf(x,0,2);
plot(x,y,x,z)
- 2.概率分布:P=normcdf(x,mu,sigma)
- 3.逆概率分布:x=norminv(P,mu,sigma). 即求出x ,使得P{X<x}=P,此命令可用来求分位数.
例3 有10台机床,每台发生故障的概率为0.08,而10台机床工作独立,每台故障只需一个维修工人排除.问至少要配备几个维修工人,才能保证有故障而不能及时排除的概率不大于5%。
解:随机变量X示发生故障的机床的台数,则 ![]()
![]()
- 4.均值与方差:[m,v]=normstat(mu,sigma)
例5 求正态分布N(3,5^2)的均值与方差
命令为:[m,v]=normstat(3,5)
结果为:m=3,v=25
- 5.随机数生成:normrnd(mu,sigma,m,n).产生m×n阶的正态分布随机数矩阵.
例6 命令:M=normrnd(0,3,100,1)
概率模型的典型案例
传送系统的效率
背景
工人将生产出的产品挂在经过他上方的空钩上运走,若工作台数固定,挂钩数量越多,传送带运走的产品越多。
在生产进入稳态后,给出衡量传送带效率的指标,研究提高传送带效率的途径。
构造一个衡量传送系统效率的指标,并建立模型来描述工人数目、钩子数量等参数的关系。
模型分析
- 进入稳态后为保证生产系统的周期性运转,应 假定工人们的生产周期相同,即每人作完一件产品后,要么恰有空钩经过他的工作台,使他可将产品挂上运走,要么没有空钩经过,迫使他放下这件产品并立即投入下件产品的生产。
- 工人们生产周期虽然相同,但稳态下每人生产完一件产品的时刻不会一致,可以认为是随机的,并且在一个周期内任一时刻的可能性相同。
- 可以用一个周期内传送带运走的产品数占产品总数的比例,作为衡量传送带效率的数量指标。
模型假设
1)n个工作台均匀排列,n个工人生产相互独立,生产周期是常数;
2)生产进入稳态,每人生产完一件产品的时刻在一个周期内是等可能的;
3)一周期内m个均匀排列的挂钩通过每一工作台的上方,到达第一个工作台的挂钩都是空的;
4)每人在生产完一件产品时都能且只能触到一只挂钩,若这只挂钩是空的,则可将产品挂上运走;若该钩非空,则这件产品被放下,退出运送系统。
模型建立
定义传送带效率为一周期内运走的产品数(记作s,待定)与生产总数 n(已知)之比,记作 D=s/n
为确定s,从工人考虑还是从挂钩考虑,哪个方便?
一周期内有m个挂钩通过每一工作台的上方
设每只挂钩为空的概率为q,则 p=1-q
设每只挂钩不被一工人触到的概率为r,则
设每只挂钩被一工人触到的概率为u,则 r=1-u
 模型解释
模型解释
传送带效率(一周期内运走产品数与生产总数之比)
若(一周期运行的)挂钩数m远大于工作台数n, 则
定义E=1-D (一周期内未运走产品数与生产总数之比)
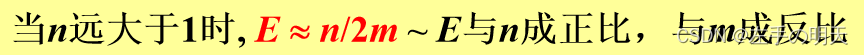
模型评注
提高效率的途径:增加m
方法一:增加一周期内通过工作台的钩子数,比如再增加m个钩子,此时钩子的总数为2m,其他条件不变:
方法二:在原来放置1只钩子处放置2只钩子,称为一个钩对,今一周期内通过m个钩对,任一钩对被一名工人触到的概率为1/m不被触到的概率为1-1/m,于是任一钩对为空的概率为
钩对上只挂上1件产品的概率为
一周期内通过的m个钩对(2m个钩子)中,空钩的平均数
于是带走产品的平均数为
未带走产品的平均数为
报童的诀窍
问题提出
报童每天清晨从报社购进报纸零售,晚上将没有卖掉的报纸退回。每份报纸
a (零售价) > b(购进价) > c(退回价)
售出一份报纸赚 a-b;退回一份报纸赔 b-c,请为报童筹划一下,每天购进多少份报纸,可使收入最大?
模型分析
报童每天购进的报纸太多,卖不完,将要赔钱。
报童每天购进的报纸太少,不够卖,会少赚钱。
 模型假设
模型假设
调查需求量的随机规律——每天需求量为 r 的概率 f(r), r=0,1,2…
设每天购进报纸 n 份,日平均收入为 G(n)
模型建立
已知售出一份赚 a-b;退回一份赔 b-c
模型求解
通常需求量r的取值和购进量n都相当大,将r视为连续型随机变量更便于分析与计算。
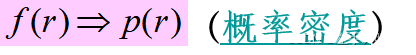
结果解释
模型评注
a-b: 售出一份赚的钱,b-c : 退回一份赔的钱,最优购进量n应使卖不完和卖完的概率之比,恰好等于卖出 一份所赚的钱与退回一份所赔的钱之比。显然当报童与报社签订的合同使报童每份赚钱与赔钱之比越大时,报童购进的份额就应越多。
模型应用
若每份报纸的购进价为b=0.75,售出价为a=1元,退回价为c=0.6,需求量服从均值为=500份,均方差为
=50份的正态分布,问报童每天应购进多少报纸才能使收入最高?
随机存贮策略
问题提出
商店在一周中的销售量是随机的。每逢周末根据库存决定是否订货,供下周销售。订货依据的一种简单策 略是制定一个下界 s和一个上界S。当周末库存小于s 时订货,否则不订货。且订货量使得下周初的存量达到 S,这种策略称为(s, S)随机存贮策略。
只考虑订货费、存贮费、缺货费、购进费,制订(s, S)存贮策略,使(平均意义下)总费用最小。
存贮策略(s, S)的优劣与总费用(平均意义下),销售量 的随机规律及单项费用有关。
模型假设
- 每次订货费c0, 每件商品购进价c1,每件商品一周贮存费c2,每件商品缺货损失费c3 (c1<c3)
- 每周销售量 r 随机、连续,概率密度 p(r)
- 周末库存量x, 订货量 u, 周初库存量 x+u
- 一周的销售是集中在周初进行的,每周贮存量按 x+u-r 计算
模型分析
按照(s, S)策略的要求:
- 当周末存贮量x≥s时,
=0,
- 当周末存贮量x<s时,
>0,且x+
=S,
确定s,S应以总费用最小为标准,因为r随机,所以贮存量与缺货量也是随机的,致使一周的贮存费和缺货费等也是随机的。所以目标函数应取一周总费用的期望值。
模型建立
模型求解
- 1)设 x<s, 求 u 使 J(u) 最小,确定S
由上式可知,S可通过概率比确定,而它使得平均费用最小。
若购进价c1一定时,贮存费c2越小,缺货费c3越大,则S应越大,这是符合常识的。
- 2)对库存 x,确定订货点s
模型评注
在这个模型中,贮存费用的计算是比较困难的,因为一般地,贮存费应与贮存时间有关,所以应对一周内贮存量的变化情况作出适当的假定。
按照模型假设4,设x=0, 贮存量Q在一周内的变化情况,如图所示
轧钢中的浪费
问题提出
把粗大的钢坯变成合格的钢材通常需要两道工序。
第一道是粗轧(热轧), 形成钢材的雏形。
第二道是精轧(冷轧),得到规定的长度成品材。
粗轧时由于受设备、环境等众多因素的影响,得到的钢材的长度是随机的,大体上呈正态分布,其均值可以在轧制过程中由轧机调整,而均方差则是由设备的精度决定的,不能随意改变。
如果粗轧后的钢材长度大于规定长度,则精轧切掉多余部分,造成浪费。
如果粗轧钢材长度小于规定长度,则整根报废,造成更大的浪费。
显然应综合考虑这两种因素,使得总的浪费最小。
模型假设
设成品材的规定长度为l和粗轧后钢材长度的均方差, 确定粗轧后钢材长度的均值m,使得当轧机调整到m进行粗轧,再通过精轧以得到的成品材时总的浪费最小。
模型分析
记粗轧时可以调整的均值为 m,则粗轧得到的钢材长度x为正态随机变量,记作 x~N(m, )
模型建立
选择合适的目标函数,并用已知的和待确定的量l, , m,把目标函数表示出来。
粗轧一根钢材总浪费=切掉多余部分的浪费+整根报废的浪费
粗轧N根钢材,所用钢材总长度mN,其中可以轧成成品材的只有PN根,成品材长度l PN。于是
浪费总长度mN-lPN,粗轧一根钢材平均浪费的长度为
得到一根成品材平均浪费的长度为
略去常数l,选取目标函数为
实际上,J(m)恰好是平均每得到一根成品材所需钢材的长度
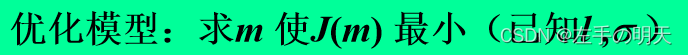
模型求解
模型应用
例 设l=2(米), =20(厘米),求m使浪费最小。
例 设l=2(米), =10(厘米),求 m 使浪费最小.
模型假定粗轧钢材长度小于规定长度l→整根报废,实际上这种钢材还常常轧成较小规格如长为 l1(<l)的成品材,只有当x<l1时才整根报废。即粗轧钢材长度在规定长度[l1, l]内降级使用,减免浪费。如何建立目标函数?
若先轧N根钢材,则成品材有NP根,降级材有NP1根,设每一根降级材可折合(<1)根成品材,那么选用每一根成品材浪费的平均长度为目标函数J,则
随机人口模型
问题提出
已知初始人口并且给定了生育率、死亡率等数据后,可以按照确定性模型确切地预测未来的人口。
但是事实上,一个人的出生与死亡可以说是随机事件,无法准确预测。
之所以应用确定性模型描述人口的发展,是因为考察的是一个国家或地区的数量很大的人口,用对总数而 言的平均生育率、死亡率代替出生、死亡的概率,将 人口作为连续型随机变量处理。
如果研究的对象是一个村落或一个家族的人口,数量不大,需作为离散型随机变量看待时,就要利用随机人口模型来描述其变化过程了。
模型假设

1)出生一人的概率与成正比,记
;出生二人及二人以上的概率为o(
)。
2)死亡一人的概率与成正比,记
;死亡二人及二人以上的概率为o(
)。
3)出生和死亡是相互独立的随机事件。
模型建立
按照全概率公式
这是一组递推微分方程,求解困难且不必要。
转而求解X(t)的期望和方差。
模型求解
模型评注
这个随机模型得到的人口期望值的结果与最简单的确定性指数增长模型的结果相对应。
本模型更积极的意义是可以描述一般的生灭过程, 如 电梯的升降、各种排队系统等。


























































 支付宝扫一扫
支付宝扫一扫 微信扫一扫
微信扫一扫







.png)



.png)
.png)

