
A-众数问题(分治算法A-D)
Description:
给定含有n个元素的多重集合S,每个元素在S中出现的次数称为该元素的重数。多重集S中重数最大的元素称为众数。例如,S={1,2,2,2,3,5}。多重集S的众数是2,其重数为3。对于给定的由n 个自然数组成的多重集S,计算S的众数及其重数。如果出现多个众数,请输出最小的那个。
Input:
输入数据的第1行是多重集S中元素个数n(n<1300000);接下来的n行中,每行有一个最多含有5位数字的自然数.
Output:
输出数据的第1行给出众数,第2行是重数。
Sample
Input :
6
1
2
2
2
3
5
Output:
2
3
代码块:
#include<bits/stdc++.h>
using namespace std;
int main(){int n;cin>>n;map<int,int> mp;for(int i=0;i<n;i++){int s;cin>>s;mp[s]++;}int max_s = -1;int t;for(auto i:mp){if(i.second>max_s){t = i.first;max_s=i.second;}}cout<<t<<endl<<max_s;return 0;
}
B – 整数因子分解问题
Description:
大于1的正整数n可以分解为:n=x1x2…xm。例如,当n=12 时,共有8 种不同的分解式:
12=12;
12=62;
12=43;
12=34;
12=322;
12=26;
12=232;
12=22*3。
对于给定的正整数n,计算n共有多少种不同的分解式。
Input:
输入数据只有一行,有1个正整数n (1≤n≤2000000000)。
Output:
将计算出的不同的分解式数输出。
Sample
Input :
12
Output:
8
代码块:
#include<bits/stdc++.h>
using namespace std;
long long a[10000000];//注意数据类型,使用map会超时,判断边界是1e7
long long zsfj(int x){long long sum=1;if(x<10000000&&a[x]){ //这里的判断条件不能颠倒顺序,否则超时return a[x];}for(int i=2;i*i<=x;i++){if(x%i==0){sum+=zsfj(i);if(i*i!=x){sum+=zsfj(x/i);}}}if(x<10000000)a[x]=sum;return sum;
}
int main(){int n;cin>>n;printf("%lld\n",zsfj(n));return 0;}
C – 顺序表应用7:最大子段和之分治递归法
Description:
给定n(1<=n<=50000)个整数(可能为负数)组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0,依此定义,所求的最优值为: Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n。 例如,当(a[1],a[2],a[3],a[4],a[5],a[6])=(-2,11,-4,13,-5,-2)时,最大子段和为20。
注意:本题目要求用分治递归法求解,除了需要输出最大子段和的值之外,还需要输出求得该结果所需的递归调用总次数。
递归调用总次数的获得,可以参考以下求菲波那切数列的代码段中全局变量count的用法:
#include
int count=0;
int main()
{
int n,m;
int fib(int n);
scanf(“%d”,&n);
m=fib(n);
printf(“%d %d\n”,m,count);
return 0;
}
int fib(int n)
{
int s;
count++;
if((n1)||(n0)) return 1;
else s=fib(n-1)+fib(n-2);
return s;
}
Input:
第一行输入整数n(1<=n<=50000),表示整数序列中的数据元素个数;
第二行依次输入n个整数,对应顺序表中存放的每个数据元素值。
Output:
一行输出两个整数,之间以空格间隔输出:
第一个整数为所求的最大子段和;
第二个整数为用分治递归法求解最大子段和时,递归函数被调用的总次数。
Sample
Input :
6
-2 11 -4 13 -5 -2
Output:
20 11
代码块:
#include<bits/stdc++.h>
using namespace std;
int a[100000];
int cnt=0;
int zdfdh(int left,int right){cnt++;if(left>=right){return a[left]>0?a[left]:0;}int mid=(left+right)/2;int rsum = zdfdh(mid+1,right); //int lsum = zdfdh(left,mid); //注意参数的传递,此处非(left,mid-1),因为在传入右侧部分时没有传入a[mid]而该函数对两侧要求是闭区间的要求所以需要左侧包含a[mid]int t=0,s=-1;for(int i=mid;i>=left;i--){t+=a[i];if(t>s){s=t;}}int t1=0,s1=-1;for(int i=mid+1;i<=right;i++){t1+=a[i];if(t1>s1){s1=t1;}}return max(lsum,max(s1+s,rsum));
}
int main(){int n;cin>>n;for(int i=0;i<n;i++){cin>>a[i];}cout<<zdfdh(0,n-1)<<" "<<cnt;return 0;
}
D – 骨牌铺方格
Description:
在2×n的一个长方形方格中,用一个1× 2的骨牌铺满方格,输入n ,输出铺放方案的总数. 例如n=3时,为2× 3方格,骨牌的铺放方案有三种,如下图:
Input:
输入包含一个整数n,表示该测试实例的长方形方格的规格是2×n (0< n<=50)。
Output:
输出铺放方案的总数。
Sample
Input :
3
Output:
3
代码块:
#include<bits/stdc++.h>
using namespace std;
long long f[1000];//注意数据类型为long long
int main(){f[1]=1;f[2]=2;int n;cin>>n;for(int i=3;i<=n;i++){f[i]=f[i-1]+f[i-2];}cout<<f[n]<<endl;return 0;
}
A – 高数Umaru系列(9)——哈士奇(动态规划A-E)
Description:
由于高数巨养的喵星人太傲娇了,要天天吃新鲜猫粮而且还经常欺负高数巨,所以高数巨决定买几条哈士奇尝尝鲜。这天高数巨来到了二手狗市场买哈士奇,高数巨看完了所有的哈士奇,记下了每条哈士奇的价格,并根据对它们的好感程度给它们每只都赋予了一个萌值。高数现在手里有X元,她想通过购买若干条哈士奇来获得尽可能多的萌值。现在给定高数巨手里的钱X以及N条哈士奇的价格和萌值,求高数巨最多可获得多少萌值
Input:
多组输入。
对于每组输入,第一行有两个整数N,X(1 < = N < = 100,1 < = X < = 1000),分别表示哈士奇的数量和高数巨的钱数
接下来的N行每行有两个整数Pi,Mi(1 < = Pi,Mi < = 100),分别表示第i条哈士奇的价格和萌值
Output:
对于每组数据,输出一个整数,表示高数巨最多可以获得的萌值,每组输出占一行
Sample
Input :
2 100
50 20
60 40
3 100
20 55
20 35
90 95
1 10
20 50
Output:
40
95
0
代码块:
#include<bits/stdc++.h>
using namespace std;
int dp[1000];
int t[1000],m[1000];
int main(){int n,x;while(~scanf("%d %d",&n,&x)){for(int i=1;i<=n;i++){cin>>t[i]>>m[i];}memset(dp,0,sizeof(dp));for(int i=1;i<=n;i++){for(int j=x;j>=t[i];j--){dp[j]=max(dp[j],dp[j-t[i]]+m[i]);}}cout<<dp[x]<<endl;}return 0;
}
B – 最少硬币问题
Description:
设有n种不同面值的硬币,各硬币的面值存于数组T[1:n]中。现要用这些面值的硬币来找钱。可以使用的各种面值的硬币个数存于数组Coins[1:n]中。
对任意钱数0≤m≤20001,设计一个用最少硬币找钱m的方法。
对于给定的1≤n≤10,硬币面值数组T和可以使用的各种面值的硬币个数数组Coins,以及钱数m,0≤m≤20001,计算找钱m的最少硬币数。
Input:
输入数据第一行中只有1个整数给出n的值,第2行起每行2个数,分别是T[j]和Coins[j]。最后1行是要找的钱数m。
Output:
输出数据只有一个整数,表示计算出的最少硬币数。问题无解时输出-1。
Sample
Input :
3
1 3
2 3
5 3
18
Output:
5
代码块:
#include<bits/stdc++.h>
#define inf 0x3f3f3f3f
using namespace std;
int t[12],c[12];//面值、数量
int dp[20010];
int main()
{int n;cin>>n;for(int i =0; i<n; i++)cin>>t[i]>>c[i];int p;cin>>p;memset(dp,inf,sizeof(dp));//顺序1dp[0] =0;//顺序2for(int i = 0; i<n; i++)for(int j = 1; j <= c[i]; j++)//钱个数量是从1开始,不可能给0张for(int k = p; k >= t[i]; k--){dp[k]=min(dp[k],dp[k-t[i]]+1);}if(dp[p] >= inf)dp[p] =-1;cout<<dp[p]<<endl;
}C – 数字三角形问题
Description:
给定一个由n行数字组成的数字三角形如下图所示。试设计一个算法,计算出从三角形的顶至底的一条路径,使该路径经过的数字总和最大。
对于给定的由n行数字组成的数字三角形,计算从三角形的顶至底的路径经过的数字和的最大值。
Input:
输入数据的第1行是数字三角形的行数n,1≤n≤100。接下来n行是数字三角形各行中的数字。所有数字在0…99之间。
Output:
输出数据只有一个整数,表示计算出的最大值。
Sample
Input :
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
Output:
30
代码块:
#include<bits/stdc++.h>
using namespace std;
int dp[105][105];
int main(){int n;cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){cin>>dp[i][j];}}for(int i=n-1;i>=1;i--){for(int j=1;j<=i;j++){dp[i][j]+=max(dp[i+1][j],dp[i+1][j+1]);}}cout<<dp[1][1]<<endl;return 0;
}
D – 最长公共子序列问题
Description:
给定两个序列 X={x1,x2,…,xm} 和 Y={y1,y2,…,yn},找出X和Y的最长公共子序列。
Input:
输入数据有多组,每组有两行 ,每行为一个长度不超过500的字符串(输入全是大写英文字母(A,Z)),表示序列X和Y。
Output:
每组输出一行,表示所求得的最长公共子序列的长度,若不存在公共子序列,则输出0。
Sample
Input :
ABCBDAB
BDCABA
Output:
4
代码块:
#include<bits/stdc++.h>
using namespace std;
char a[505];
char b[505];
int dp[505][505];
int main(){while(~scanf("%s\n%s",a+1,b+1)){memset(dp,0,sizeof(dp));int l1=strlen(a+1);int l2=strlen(b+1);for(int i=1;i<=l1;i++){for(int j=1;j<=l2;j++){if(a[i]==b[j]){dp[i][j]=dp[i-1][j-1]+1;}else{dp[i][j] = max(dp[i][j-1],dp[i-1][j]);}}}cout<<dp[l1][l2]<<endl;}return 0;
}
E – 石子合并问题
Description:
在一个圆形操场的四周摆放着n堆石子。现要将石子有次序地合并成一堆。规定每次只能选相邻的2 堆石子合并成新的一堆,并将新的一堆石子数记为该次合并的得分。试设计一个算法,计算出将n堆石子合并成一堆的最小得分和最大得分。
对于给定n堆石子,计算合并成一堆的最小得分和最大得分。
Input:
输入数据的第1行是正整数n,1≤n≤100,表示有n堆石子。第二行有n个数,分别表示每堆石子的个数。
Output:
输出数据有两行,第1行中的数是最小得分,第2行中的数是最大得分。
Sample
Input :
4
4 4 5 9
Output:
43
54
代码块:
#include <iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
#define INF 0x3f3f3f
int stone[105];
int dpmin[205][205];//最小
int dpmax[205][205];//最大
int sum[205];
int main()
{int n;scanf("%d",&n);memset(sum,0,sizeof(sum));memset(dpmin,INF,sizeof(dpmin));memset(dpmax,-1,sizeof(dpmax));for(int i =1;i<=n;i++){scanf("%d",&stone[i]);sum[i] = sum[i - 1] + stone[i];dpmin[i][i] = 0;dpmax[i][i] = 0;}for(int i = 1;i<=n;i++){sum[i+n] = sum[i+n-1]+stone[i];//展开的n后面的n-1~1重量dpmin[i+n][i+n] = 0;dpmax[i+n][i+n] = 0;}for(int len = 2;len<=n;len++){//长度还是最大nfor(int j = 1;j+len-1<=2*n-1;j++){//起点枚举最大到2*n-1,ends<=2*n-1int ends = j+len - 1;for(int i = j;i<ends;i++){//注意!i<ends!!!因为i=ends时,dp[ends+1][ends]是不成立的!dpmin[j][ends] = min(dpmin[j][ends],dpmin[j][i]+dpmin[i+1][ends]+sum[ends]-sum[j-1]);dpmax[j][ends] = max(dpmax[j][ends],dpmax[j][i]+dpmax[i+1][ends]+sum[ends]-sum[j-1]);}}}int ansmin = 0xfffffff;int ansmax = -1;for(int i = 1;i<=n;i++){ansmin = min(ansmin,dpmin[i][i+n-1]);//找1~n,2~n~1,3~n~2....的合并n个堆的中最大和最小的值ansmax = max(ansmax,dpmax[i][i+n-1]);}cout<<ansmin<<endl;cout<<ansmax<<endl;return 0;
}
A – 汽车加油问题(贪心A-F)
Description:
一辆汽车加满油后可行驶n公里。旅途中有若干个加油站。设计一个有效算法,指出应在哪些加油站停靠加油,使沿途加油次数最少。并证明算法能产生一个最优解。
对于给定的n和k个加油站位置,计算最少加油次数。
Input:
输入数据的第一行有2 个正整数n和k(n≤5000,k≤1000),表示汽车加满油后可行驶n公里,且旅途中有k个加油站。接下来的1 行中,有k+1 个整数,表示第k个加油站与第k-1 个加油站之间的距离。第0 个加油站表示出发地,汽车已加满油。第k+1 个加油站表示目的地。
Output:
将计算出的最少加油次数输出。如果无法到达目的地,则输出“No Solution!”。
Sample
Input :
7 7
1 2 3 4 5 1 6 6
Output:
4
代码块:
#include<bits/stdc++.h>
using namespace std;
int dis[5005];
int main(){int n,k;cin>>n>>k;for(int i=1;i<=k+1;i++){cin>>dis[i];}//dis[i]代表i与i-1之间的距离dis[1]表示出发地到第一个加油站的距离int y1 = n;int cnt = 0;int i=0;while(i<=k){if(y1>=dis[i+1]){y1-=dis[i+1];i++;}else{if(y1<dis[i+1]){if(n>=dis[i+1]){y1=n-dis[i+1];cnt++;i++;}else{cout<<"No Solution!";return 0;}}}}cout<<cnt<<endl;return 0;
}
B – 多元Huffman编码问题
Description:
在一个操场的四周摆放着n堆石子。现要将石子有次序地合并成一堆。规定每次至少选2 堆最多选k堆石子合并成新的一堆,合并的费用为新的一堆的石子数。试设计一个算法,计算出将n堆石子合并成一堆的最大总费用和最小总费用。
对于给定n堆石子,计算合并成一堆的最大总费用和最小总费用。
Input:
输入数据的第1 行有2 个正整数n和k(n≤100000,k≤10000),表示有n堆石子,每次至少选2 堆最多选k堆石子合并。第2 行有n个数(每个数均不超过 100),分别表示每堆石子的个数。
Output:
将计算出的最大总费用和最小总费用输出,两个整数之间用空格分开。
Sample
Input :
7 3
45 13 12 16 9 5 22
Output:
593 199
代码块:
#include<bits/stdc++.h>
using namespace std;
int main()
{priority_queue<int,vector<int>,greater<int> >q1;//优先队列(从小到大)priority_queue<int>q2;//优先队列(默认从大到小)int n,k;cin>>n>>k;for(int i =0; i<n; i++){int x;cin>>x;q1.push(x);q2.push(x);}while(q1.size()%(k-1)!=1)q1.push(0);long long sum_ma =0,sum_mi =0;while(q1.size()>1){long long sum = 0;for(int i=0; i<k; i++){sum+=q1.top();q1.pop();}sum_mi +=sum;q1.push(sum);}while(q2.size()>1){int a =q2.top();q2.pop();int b =q2.top();q2.pop();sum_ma +=a+b;q2.push(a+b);}cout<<sum_ma<<" "<<sum_mi<<endl;
}C – 装船问题
Description:
王小二毕业后从事船运规划工作,吉祥号货轮的最大载重量为M吨,有10种货物可以装船。第i种货物有wi吨,总价值是pi。王小二的任务是从10种货物中挑选若干吨上船,在满足货物总重量小于等于M的前提下,运走的货物的价重比最大。
Input:
输入数据的第一行有一个正整数M(0 < M < 10000),表示所有货物最大载重量。在接下来的10行中,每行有若干个数(中间用空格分开),第i行表示的是第i种货物的货物的总价值pi ,总重量wi。(pi是wi的整数倍,0 < pi , wi < 1000)
Output:
输出一个整数,表示可以得到的最大价值。
Sample
Input :
100
10 10
20 10
30 10
40 10
50 10
60 10
70 10
80 10
90 10
100 10
Output:
550
代码块:
#include<bits/stdc++.h>
using namespace std;
struct yc{int weight;int price;double w_p;
}a[20];
bool cmp(yc a,yc b){return a.w_p>b.w_p;
}
int main(){int m;cin>>m;for(int i=0;i<10;i++){cin>>a[i].price>>a[i].weight;a[i].w_p = a[i].price/a[i].weight;}sort(a,a+10,cmp);int sum=0;for(int i=0;i<10;i++){if(m>=a[i].weight){m-=a[i].weight;sum+=a[i].price;}else{if(m<a[i].weight){sum+=a[i].w_p*m;m=0;}}if(m==0)break;}printf("%d",sum);return 0;
}
D – 活动选择
Description:
学校的大学生艺术中心周日将面向全校各个学院的学生社团开放,但活动中心同时只能供一个社团活动使用,并且每一个社团活动开始后都不能中断。现在各个社团都提交了他们使用该中心的活动计划(即活动的开始时刻和截止时刻)。请设计一个算法来找到一个最佳的分配序列,以能够在大学生艺术中心安排不冲突的尽可能多的社团活动。
比如有5个活动,开始与截止时刻分别为:
最佳安排序列为:1,4,5。
Input:
第一行输入活动数目n(0<n<100);
以后输入n行,分别输入序号为1到n的活动使用中心的开始时刻a与截止时刻b(a,b为整数且0<=a,b<24,a,b输入以空格分隔)。
Output:
输出最佳安排序列所包含的各个活动(按照活动被安排的次序,两个活动之间用逗号分隔),如果有多个活动安排序列符合要求输出字典序最小的序列。
Sample
Input :
6
8 10
9 16
11 16
14 15
10 14
7 11
Output:
1,5,4
代码块:
#include<bits/stdc++.h>
using namespace std;
struct node{int start;int end;int id;
}a[102];
bool cmp(node a,node b){return a.end==b.end?a.id<b.id:a.end<b.end;
}
int main(){int n;cin>>n;for(int i=0;i<n;i++){cin>>a[i].start>>a[i].end;a[i].id=i+1;}sort(a,a+n,cmp);cout<<a[0].id;int end1=a[0].end;for(int i=1;i<n;i++){if(a[i].start>=end1){cout<<","<<a[i].id;end1 = a[i].end;}}return 0;
}
E – 最优合并问题
Description:
给定k 个排好序的序列s1 , s2,……, sk , 用2 路合并算法将这k 个序列合并成一个序列。假设所采用的2 路合并算法合并2 个长度分别为m和n的序列需要m + n -1次比较。试设计一个算法确定合并这个序列的最优合并顺序,使所需的总比较次数最少。
为了进行比较,还需要确定合并这个序列的最差合并顺序,使所需的总比较次数最多。
对于给定的k个待合并序列,计算最多比较次数和最少比较次数合并方案。
Input:
输入数据的第一行有1 个正整数k(k≤1000),表示有k个待合并序列。接下来的1 行中,有k个正整数,表示k个待合并序列的长度。
Output:
输出两个整数,中间用空格隔开,表示计算出的最多比较次数和最少比较次数。
Sample
Input :
4
5 12 11 2
Output:
78 52
代码块:
#include<bits/stdc++.h>
using namespace std;
priority_queue<int,vector<int>,greater<int>> q1;//小顶堆
priority_queue<int> q2;//大顶堆
int main(){int n;cin>>n;for(int i=0;i<n;i++){int x;cin>>x;q1.push(x);q2.push(x);}int misum=0,masum=0;while(q1.size()!=1){int sum=0;int a=q1.top();q1.pop();int b=q1.top();q1.pop();sum=a+b;misum+=(sum-1);q1.push(sum);sum = 0;a=q2.top();q2.pop();b=q2.top();q2.pop();sum=a+b;q2.push(sum);masum+=(sum-1);}cout<<masum<<" "<<misum<<endl;
}
F – 区间覆盖问题
Description:
设x1 , x2 ,…… , xn 是实直线上的n 个点。用固定长度的闭区间覆盖这n 个点,至少需要多少个这样的固定长度闭区间?
对于给定的实直线上的n个点和闭区间的长度k,设计解此问题的有效算法,计算覆盖点集的最少区间数,并证明算法的正确性。
Input:
输入数据的第一行有2 个正整数n和k(n≤10000,k≤100),表示有n个点,且固定长度闭区间的长度为k。接下来的1 行中,有n个整数,表示n个点在实直线上的坐标(可能相同)。
Output:
输出一个整数,表示计算出的最少区间数输出。
Sample
Input :
7 3
1 2 3 4 5 -2 6
Output:
3
代码块:
#include<bits/stdc++.h>
using namespace std;
int a[100005];
bool cmp(int a,int b){return a<b;
}
int main(){int n,k;cin>>n>>k;for(int i=0;i<n;i++){cin>>a[i];}sort(a,a+n,cmp);int end = a[0]+k;int cnt = 1;for(int i=1;i<n;i++){if(end<a[i]){end=a[i]+k;cnt++;}}cout<<cnt<<endl;return 0;
}
A – 子集和问题(搜索算法A-D)
Description:
子集和问题的一个实例为〈S,t〉。其中,S={ x1 , x2 ,…,xn }是一个正整数的集合,c是一个正整数。子集和问题判定是否存在S的一个子集S1,使得:
试设计一个解子集和问题的回溯法。
对于给定的正整数的集合S={ x1 , x2 ,…,xn }和正整数c,计算S 的一个子集S1,使得:
。
Input:
输入数据的第1 行有2 个正整数n 和c(n≤10000,c≤10000000),n 表示S 的大小,c是子集和的目标值。接下来的1 行中,有n个正整数,表示集合S中的元素。
Output:
将子集和问题的解输出。当问题无解时,输出“No Solution!”。
Sample
Input :
5 10
2 2 6 5 4
Output:
2 2 6
代码块:
#include<bits/stdc++.h>
using namespace std;
int a[10005];//数组a用来存放集合S的数据
int n,c,sum;
int flag=0;//设立一个标识符,当有解时flag=1
int ans[10005]={0};//数组ans用来存放Search过程中的中转数组以及最后的输出数组
void print(int len)//输出
{for(int i=0;i<len;i++){if(i==len-1)std::cout<<ans[i]<<std::endl;elsestd::cout<<ans[i]<<" ";}
}
void Search(int x,int sum,int len)//递归调用Search函数,x是Search的起始位置
{if(sum>c||flag)//相加的和大于了c表示集合中没有可以匹配的对象,或者flag=1,有匹配对象,return跳出return ;if(sum==c){print(len);flag=1;return ;}for(int i=x;i<n;i++){if(a[i]+sum<=c){ans[len]=a[i];Search(i+1,sum+a[i],len+1);//递归调用}}
}
int main()
{std::cin>>n>>c;sum=0;for(int i=0;i<n;i++){std::cin>>a[i];sum+=a[i];}if(sum<c)//首先判断所有元素的和是否小于c,小于c的话必然无解std::cout<<"No Solution!"<<std::endl;else{Search(0,0,0);if(!flag)std::cout<<"No Solution!"<<std::endl;}return 0;
}
B – 运动员最佳匹配问题
Description:
羽毛球队有男女运动员各n 人。给定2 个n×n 矩阵P 和Q。P[i][j]是男运动员i 和女运动员j配对组成混合双打的男运动员竞赛优势;Q[i][j]是女运动员i和男运动员j配合的女运动员竞赛优势。由于技术配合和心理状态等各种因素影响,P[i][j]不一定等于Q[j][i]。男运动员i和女运动员j配对组成混合双打的男女双方竞赛优势为P[i][j]*Q[j][i]。
设计一个算法,计算男女运动员最佳配对法,使各组男女双方竞赛优势的总和达到最大。
设计一个算法,对于给定的男女运动员竞赛优势,计算男女运动员最佳配对法,使各组男女双方竞赛优势的总和达到最大。
Input:
输入数据的第一行有1 个正整数n (1≤n≤20)。接下来的2n 行,每行n个数。前n行是p,后n行是q。
Output:
将计算出的男女双方竞赛优势的总和的最大值输出。
Sample
Input :
3
10 2 3
2 3 4
3 4 5
2 2 2
3 5 3
4 5 1
Output:
52
代码块:
#include<bits/stdc++.h>
using namespace std;
int x[25][25],y[25][25];
int maxsum[25];//用来剪枝
int tmp[25][25];
int vis[25];
int sum,Max,n;
void dfs(int x)
{if(x>=n)//都遍历完,更新Max为当前搜索sum和Max的最大值{Max=max(sum,Max);return ;}int cnt=0;for(int i=x; i<n; i++) //cnt存放从x到n个男生的最大优势和(有可能女生重复匹配)cnt+=maxsum[i];if(sum+cnt<=Max) return ;//如果Max已经大于当前搜索值sum+congx到n的假设匹配最大优势和cnt;Max已经足够大,不需要再继续搜索for(int i=0; i<n; i++) //搜索男生x和女生i的的最佳优势(因为vis[i]表示女生是否被匹配过,男女匹配不会重){if(!vis[i]){vis[i]=1;sum+=tmp[x][i];dfs(x+1);sum-=tmp[x][i];vis[i]=0;}}
}
int main()
{cin>>n;for(int i=0; i<n; i++){for(int j=0; j<n; j++){cin>>x[i][j];}}for(int i=0; i<n; i++){for(int j=0; j<n; j++){cin>>y[i][j];}}for(int i=0; i<n; i++){for(int j=0; j<n; j++){tmp[i][j]=x[i][j]*y[j][i];//存放男生i和女生j匹配的优势maxsum[i]=max(maxsum[i],tmp[i][j]);//存放男生i的最大优势。但maxsum匹配出来的男女生有可能会有重复,所以要用一个vis标记有没有被访问过,在dfs中遍历}}Max=0;sum=0;memset(vis,0,sizeof(vis));dfs(0);cout<<Max<<endl;return 0;
}
C – 工作分配问题
Description:
设有n件工作分配给n个人。将工作i分配给第j个人所需的费用为 cij。试设计一个算法,为每一个人都分配1 件不同的工作,并使总费用达到最小。
设计一个算法,对于给定的工作费用,计算最佳工作分配方案,使总费用达到最小。
Input:
输入数据的第一行有1 个正整数n (1≤n≤11)。接下来的n行,每行n个数,表示工作费用。
Output:
将计算出的最小总费用输出。
Sample
Input :
3
10 2 3
2 3 4
3 4 5
Output:
9
代码块:
#include <iostream>
using namespace std;
#define inf 0x3f3f3f3fint n, ans;
int c[25][25];
int vis[25];void dfs(int i, int sum)//i是行号
{if (sum > ans) //剪枝return;if (i == n + 1 && sum < ans){ans = sum;return;}for (int j = 1; j <= n; j++){if (!vis[j])//遍历第i行 没有被遍历过列号j 的元素{vis[j] = 1;dfs(i + 1, sum + c[i][j]);vis[j] = 0;}}
}
int main()
{cin >> n;for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++)cin >> c[i][j];ans = inf;dfs(1, 0);cout << ans << endl;return 0;}
D – 整数变换问题
Description:
整数变换问题。关于整数i的变换f和g定义如下:f(i)=3i;
试设计一个算法,对于给定的2 个整数n和m,用最少的f和g变换次数将n变换为m。例如,可以将整数15用4 次变换将它变换为整数4:4=gfgg(15)。当整数n不可能变换为整数m时,算法应如何处理?
对任意给定的整数n和m,计算将整数n变换为整数m所需要的最少变换次数。
Input:
输入数据的第一行有2 个正整数n和m。n≤100000,m≤1000000000。
Output:
将计算出的最少变换次数以及相应的变换序列输出。第一行是最少变换次数。第2 行是相应的变换序列。
Sample
Input :
15 4
Output:
4
gfgg
代码块:
#include<bits/stdc++.h>
using namespace std;
char s[105];
int len;
int maxsum;
int select(int i,int n,int m)
{if(i==0)return 3*n;elsereturn n/2;
}
int dfs(int step,int n,int m)
{if(step>maxsum)return 0;for(int i=0;i<2;i++){int num=select(i,n,m);if(num==m||dfs(step+1,num,m))//dfs返回1说明匹配到n==m{if(i==0){s[len++]='f';//为什么先走乘法??}else{s[len++]='g';}return 1;}}return 0;
}
int main()
{int n,m;cin>>n>>m;len=0;maxsum=1;while(!dfs(1,n,m))//达到剪枝效果{maxsum++;}cout<<maxsum<<endl;for(int i=0;i<len;i++){cout<<s[i];}cout<<endl;return 0;
}




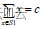
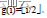
 支付宝扫一扫
支付宝扫一扫 微信扫一扫
微信扫一扫







.png)

.png)

