一、行列式的公式

　以二阶行列式为例：我们可以这么做$a=a+0, b=0+b, c=c+0, d=0+d$，则

　在反复利用行列式的单行可拆性后，A分解成4项，每一行只有一个非零元素。二阶行列式计计算的是图形的面积

　对于α来说，由于构成行列式的两个向量<a, 0>和<c, 0>是在同一个维度上的直线，所以二者围成的面积是0；同理，δ也一样

　最终：$|A|=ad – bc$

　这种方法对于更高阶的行列式也同样适用，三阶行列式按照每一行只有一个非零元素的原则全部展开后将长达33项，这将占用长长的篇幅

　可以考虑一个能够缩减展开式的办法。根据行列式的几何意义，行列式计算的是n维图形在n维空间中的n维体积，3阶行列式计算的自然是三维空间的体积

　如此一来，只有三个向量分别指向三个不同维度时，才能保证体积不等于0，因此三阶行列式可以展开成：

　

　现在只剩下3! = 6项，每一项都可以通过行列式的行交换性质变成上三角行列式（或者本身就是上三角行列式），这样就可以得到行列式的最终值：

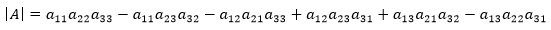
　现在可以归纳出n阶行列式的公式：

　下标的数字项表示行号，希腊字母表示列号（实际数量可能远超过希腊字母的数量，暂且用希腊字母代替）。这相当于是列号的排列，在每一项中，n个列标都各用一次。负号的目的是为了应对行交换的情况。

　根据公式，对于n阶单位矩阵来说，只有主对角线的一项不是0，所以单位矩阵的行列式的值是1

　示例 计算A的行列式：

　通过消元法计算是正确的选择，通常也应该这么做，实际上不难看出这个A是一个奇异矩阵，所以它的行列式等于0

　现在用行列式的公式来验证这个结论。根据公式， $|A|$的大多数展开项都等0，没有被淘汰的只有两项，二者相加等于0：

　第一个行列式是负值，因为它需要用1、3行进行一次行交换来变成上三角矩阵：

二、代数余子式

　代数余子式是从行列式的公式中提取出来的，它的作用是把$n$阶行列式化简为$n – 1$阶行列式。我们以三阶行列式为例，看看代数余子式是什么。根据行列 式的公式，3阶行列式展开，将得到：

$|A|=a_{11}left(a_{22} a_{33}-a_{23} a_{32}ight)-a_{12}left(a_{21} a_{33}-a_{23} a_{31}ight)+a_{13}left(a_{21} a_{32}-a_{22} a_{31}ight)$

　这实际上式选定第一行的一列，然后考虑各种可能的排列，为了突出重点，写成下面这样：

$|A|=a_{11}left(……ight)-a_{12}left(……ight)+a_{13}left(……ight)$

　注：根据第任何一行展开都将得到同样的结果，下面是根据第二行展开：

$|A|=-a_{21}left(a_{12} a_{33}-a_{13} a_{32}ight)+a_{22}left(a_{11} a_{33}-a_{13} a_{31}ight)-a_{23}left(a_{11} a_{32}-a_{12} a_{31}ight)$

　按列展开也可以，比如按第一列展开：

$|A|=a_{11}left(a_{22} a_{33}-a_{23} a_{32}ight)-a_{21}left(a_{12} a_{33}-a_{13} a_{32}ight)+a_{31}left(a_{12} a_{23}-a_{13} a_{22}ight)$

　括号中由剩余因子组成的表达式就是代数余子式（第二项把符号移到了括号中，下节会说明原因），比如$a_{22} a_{33}-a_{23} a_{32}$是$a_{11}$的代数余子式。可以用更直观的方式表达$a_{11}(a_{22} a_{33}-a_{23} a_{32})$

$a_{11}left(a_{22} a_{33}-a_{23} a_{32}ight)=a_{11}left|egin{array}{ll}{a_{22}} & {a_{23}} \ {a_{32}} & {a_{33}}end{array}ight|=left|egin{array}{ccc}{a_{11}} & {square} & {1} \ {square} & {a_{22}} & {a_{23}} \ {square} & {a_{32}} & {a_{33}}end{array}ight|$

 

三、代数余子式的符号

　$-a_{12}left(a_{21} a_{33}-a_{23} a_{31}ight)$可以表示为：

$-a_{12}left(a_{21} a_{33}-a_{23} a_{31}ight)=-a_{12}left|egin{array}{ll}{a_{21}} & {a_{23}} \ {a_{31}} & {a_{33}}end{array}ight|=left|egin{array}{ccc}{square} & {a_{12}} & {square} \ {a_{21}} & {square} & {a_{23}} \ {a_{31}} & {square} & {a_{33}}end{array}ight|$

　注意到上式有一个负号，我们一般不需要$-a_{12}$的代数余子式，所以$a_{12}$的代数余子式需要把符号移到括号中：

$-a_{12}left(a_{21} a_{33}-a_{23} a_{31}ight)=a_{12}left(-a_{21} a_{33}+a_{23} a_{31}ight)$

　代数余子式本身就是行列式，只是它的正负号需要单独判断，判断方法是根据选定元素行号和列号之和的奇偶性。用$C_{ij}$表示$a_{ij}$的代数余子式，当$i + j$是偶数时，行列式取正号，是奇数则取负号，比如三阶行列式中$C_{12}$的行列号之和是3，它对应的代数余子式取负号。如果有一个五阶行列式，它的每一项的代数余子式的符号是这样分布的：

$left|egin{array}{cccc}{+} & {-} & {+} & {-} & {+} \ {-} & {+} & {-} & {+} & {-} \ {+} & {-} & {+} & {-} & {+} \ {-} & {+} & {-} & {+} & {-} \ {+} & {-} & {+} & {-} & {+}end{array}ight|$

 

四、行列式的代数余子式展开

　把某个行列式的用代数余子式展开实际上也是求行列式的另一种方法，可以表示成：

$|A|=a_{11} C_{11}+a_{12} C_{12}+cdots a_{1 n} C_{1 n}=sum_{i=1}^{n} a_{1 i} C_{1 i}$

　代数余子式本身是$n – 1$阶行列式，它可以继续展开成$n – 2$阶行列式……如此展开下去，直到1阶行列式为止，其核心思想是把一个复杂的高阶行列式转换成多个简单的低阶行列式

　由于行列式根据任何一行展开都可以，所以：

$|A|=a_{k 1} C_{k 1}+a_{k 2} C_{k 2}+cdots a_{k n} C_{k n}=sum_{i=1}^{n} a_{k i} C_{k i}$

 

五、二阶行列式的代数余子式

　用代数余子式可以解释二阶行列式的计算公式。二阶行列式可以用一阶代数余子式展开：

$left|egin{array}{ll}{a} & {b} \ {c} & {d}end{array}ight|=aleft|egin{array}{cc}{square} & {square} \ {square} & {d}end{array}ight|-bleft|egin{array}{cc}{square} & {square} \ {c} & {square}end{array}ight|=a d-b c$

　由于$b$是第1行第2列，$1 + 2 = 3$是奇数，所以$b$对应的代数余子式$C_{12}$是以负号开头的

 

六、致谢

　本文参考，感谢作者分享，知识共享改变世界！